Частные производные
Определение.Частной производной функции 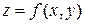 по переменной
по переменной 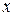 в точке
в точке 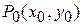 называется предел отношения частного приращения функции
называется предел отношения частного приращения функции 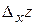 к соответствующему приращению аргумента
к соответствующему приращению аргумента 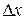 , когда последнее произвольным образом стремится к нулю, т.е.
, когда последнее произвольным образом стремится к нулю, т.е.
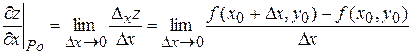 .
.
Используются также и другие обозначения частных производных: 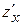 ,
, 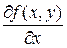 ,
, 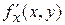 .
.
Аналогично определяют и частную производную функции 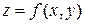 в точке
в точке 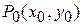 по переменной
по переменной 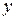 :
:
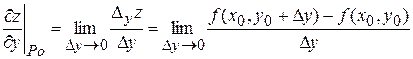 .
.
Таким образом, частная производная функции нескольких переменных определяется как производная функции одной переменной при фиксированных значениях остальных переменных.
Пример.Найти частные производные функции 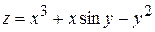 .
.
Решение.Частную производную функции 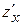 вычисляем как производную данной функции по переменной
вычисляем как производную данной функции по переменной 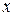 , считая
, считая 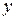 постоянной:
постоянной:
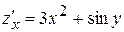 . Аналогично
. Аналогично 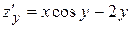 .
.
Пример.Найти частные производные функции 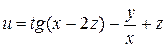 .
.
Решение.Частную производную функции 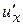 вычисляем как производную данной функции по переменной
вычисляем как производную данной функции по переменной 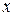 , считая
, считая 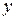 и
и 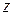 постоянными:
постоянными:
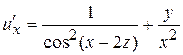 .
.
Аналогично 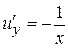 и
и 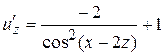 .
.
Геометрический смысл частных производных функции двух переменных.Пусть графиком функции 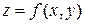 является некоторая поверхность Q. Возьмем точку
является некоторая поверхность Q. Возьмем точку 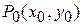 Î D
Î D 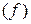 . На этой поверхности ей соответствует точка
. На этой поверхности ей соответствует точка 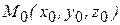 . Пересечем график данной функции плоскостью
. Пересечем график данной функции плоскостью 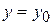 . В сечении получим кривую
. В сечении получим кривую 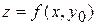 ( на рисунке это кривая
( на рисунке это кривая 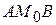 ), которую можно рассматривать как график функции одной переменной
), которую можно рассматривать как график функции одной переменной 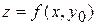 в плоскости
в плоскости 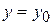 .
.
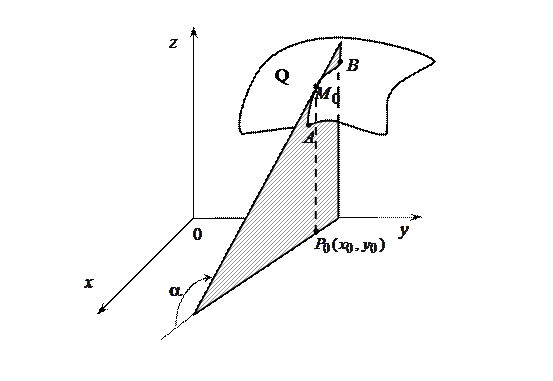
Тогда, согласно геометрическому смыслу производной функции одной переменной, значение частной производной 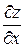 функции
функции 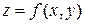 в точке
в точке 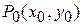 равно тангенсу угла α, образованного положительным направлением оси Ох и касательной, проведенной в точке
равно тангенсу угла α, образованного положительным направлением оси Ох и касательной, проведенной в точке 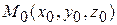 к линии пересечения поверхности
к линии пересечения поверхности 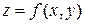 и плоскости
и плоскости 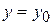 .
.
Аналогично трактуется и геометрический смысл частной производной функции 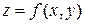 по
по 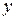 .
.
Механический смысл частных производных функции двух переменных.Частные производные 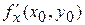 и
и  характеризуют скорость изменения функции
характеризуют скорость изменения функции 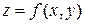 в данной точке
в данной точке 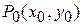 , причем частная производная
, причем частная производная 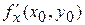 задает скорость изменения функции в направлении прямой
задает скорость изменения функции в направлении прямой 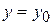 , частная производная
, частная производная  ― в направлении прямой
― в направлении прямой 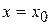 .
.
Дата добавления: 2021-01-11; просмотров: 467;











