Коэффициентом отражения
Коэффициентом пропускания
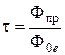 , (5)
, (5)
коэффициентом отражения
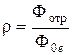 (6)
(6)
и коэффициентом поглощения
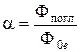 , (7)
, (7)
где 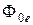 – –
| поток (мощность) падающего излучения; |
| Фпр – | поток прошедшего излучения; |
| Фотр – | поток отражённого излучения; |
| Фпогл – | поток поглощённого излучения. |
Коэффициенты t, r и a зависят от свойств самого тела и длины волны падающего излучения. Спектральная зависимость, т.е. зависимость коэффициентов от длины волны, определяет цвет как прозрачных, так и непрозрачных (t= 0) тел.
Согласно закону сохранения энергии
Фотр + Фпогл + Фпр = 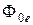 . (8)
. (8)
Разделив обе части равенства на 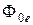 , получим:
, получим:
r + a +t = 1. (9)
Тело, для которого r=0, t=0, a=1 называется абсолютно чёрным.
Абсолютно черное тело при любой температуре полностью поглощает всю энергию падающего на него излучения любой длины волны. Все реальные тела не являются абсолютно черными. Однако некоторые из них в определенных интервалах длин волн близки по своим свойствам к абсолютно черному телу. Например, в области длин волн видимого света коэффициенты поглощения сажи, платиновой черни и черного бархата мало отличаются от единицы. Наиболее совершенной моделью абсолютно чёрного тела может служить малое отверстие в замкнутой полости. Очевидно, что эта модель тем ближе по характеристикам к черному телу, чем больше отношение площади поверхности полости к площади отверстия (рис. 1).
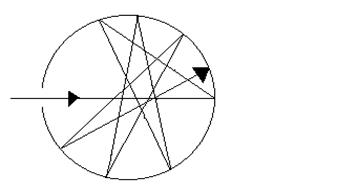
Рис. 1
Спектральной характеристикой поглощения электромагнитных волн телом является спектральный коэффициент поглощения al – величина, определяемая отношением поглощённого телом потока излучения в малом спектральном интервале (от l до l + dl) к потоку падающего на него излучения в том же спектральном интервале:
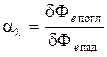 . (10)
. (10)
Излучательная и поглощательная способности непрозрачного тела взаимосвязаны. Отношение спектральной плотности энергетической светимости равновесного излучения тела к его спектральному коэффициенту поглощения не зависит от природы тела; для всех тел оно является универсальной функцией длины волны и температуры (законКирхгофа):
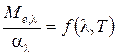 . (11)
. (11)
Для абсолютно чёрного тела al = 1. Поэтому из закона Кирхгофа следует, что Ме,l = 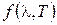 , т.е. универсальная функция Кирхгофа
, т.е. универсальная функция Кирхгофа 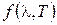 представляет собой спектральную плотность энергетической светимости абсолютно чёрного тела.
представляет собой спектральную плотность энергетической светимости абсолютно чёрного тела.
Таким образом, согласно закону Кирхгофа, для всех тел отношение спектральной плотности энергетической светимости к спектральному коэффициенту поглощения равно спектральной плотности энергетической светимости абсолютно чёрного тела при тех же значениях T и l.
Из закона Кирхгофа следует, что спектральная плотность энергетической светимости любого тела в любой области спектра всегда меньше спектральной плотности энергетической светимости абсолютно чёрного тела (при одних и тех же значениях длины волны и температуры). Кроме того, из этого закона вытекает, что если тело при некоторой температуре не поглощает электромагнитные волны в интервале от l до l + dl, то оно их в этом интервале длин при данной температуре и не излучает.
Аналитический вид функции 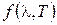 для абсолютно черного тела
для абсолютно черного тела
был установлен Планком на основе квантовых представлений о природе излучения:
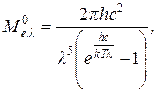 (12)
(12)
| где l – | длина волны излучения; |
| Т – | температура излучающего тела; |
с = 3×108 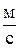 – –
| скорость света в вакууме; |
k = 1,38×10-23 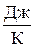 – –
| постоянная Больцмана; |
| h = 6,63×10-34 Дж×с – | постоянная Планка. |
 Спектр излучения абсолютно черного тела имеет характерный максимум (рис. 2), который при повышении температуры сдвигается в коротковолновую часть (рис. 3). Положение максимума спектральной плотности энергетической светимости можно определить из выражения (12) обычным способом, приравняв к нулю первую производную:
Спектр излучения абсолютно черного тела имеет характерный максимум (рис. 2), который при повышении температуры сдвигается в коротковолновую часть (рис. 3). Положение максимума спектральной плотности энергетической светимости можно определить из выражения (12) обычным способом, приравняв к нулю первую производную:
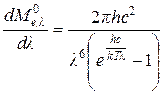
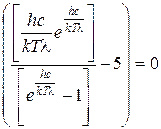 . (13)
. (13)
Обозначив 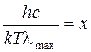 , получим:
, получим:
х 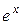 – 5 (
– 5 ( 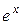 – 1) = 0. (14)
– 1) = 0. (14)

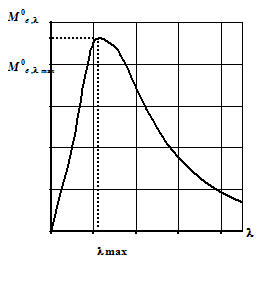
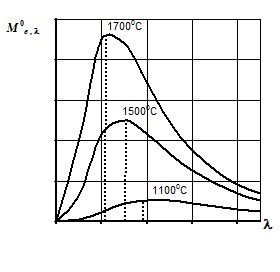
Рис. 2 Рис. 3
Решение этого трансцендентного уравнения численным методом дает
х = 4, 965.
Следовательно,
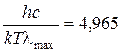 , (15)
, (15)
откуда
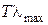 =
= 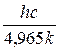 = b1 = 2, 898·
= b1 = 2, 898· 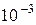 м·K, (16)
м·K, (16)
lmax= 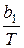 . (17)
. (17)
Таким образом, функция 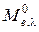 достигает максимума при длине волны, обратно пропорциональной термодинамической температуре абсолютно черного тела (первый закон Вина).
достигает максимума при длине волны, обратно пропорциональной термодинамической температуре абсолютно черного тела (первый закон Вина).
Из закона Вина следует, что при низких температурах излучаются преимущественно длинные (инфракрасные) электромагнитные волны. По мере же возрастания температуры увеличивается доля излучения, приходящаяся на видимую область спектра, и тело начинает светиться. С дальнейшим ростом температуры яркость его свечения увеличивается, а цвет изменяется. Поэтому цвет излучения может служить характеристикой температуры излучения. Примерная зависимость цвета свечения тела от его температуры приведена в табл. 1.
Таблица 1
| Цвет излучения | Красный, едва видимый | Тёмно-красный | Вишнёво-красный | Оранжевый | Белый |
| Температура, ºС |
Первый закон Вина называют так же законом смещения, подчёркивая тем самым, что с ростом температуры максимум спектральной плотности энергетической светимости сдвигается в сторону меньших длин волн.
Подставив формулу (17) в выражение (12), нетрудно показать, что максимальное значение функции 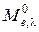 пропорционально пятой степени термодинамической температуры тела (второй закон Вина):
пропорционально пятой степени термодинамической температуры тела (второй закон Вина):
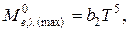
где 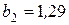 ·
· 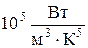 .
.
Энергетическую светимость абсолютно черного тела можно найти из выражения (12) простым интегрированием по длине волны
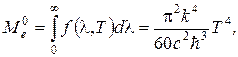 (18)
(18)
где 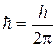 – приведенная постоянная Планка,
– приведенная постоянная Планка,
или
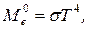 (19)
(19)
где 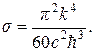
Энергетическая светимость абсолютно чёрного тела пропорциональна четвёртой степени его термодинамической температуры. Это положение носит название закона Стефана – Больцмана, а коэффициент пропорциональности s = 5,67×10-8 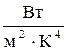 – постоянной Стефана – Больцмана.
– постоянной Стефана – Больцмана.
Абсолютно чёрное тело является идеализацией реальных тел. Реальные тела испускают излучение, спектр которого не описывается формулой Планка. Их энергетическая светимость, кроме температуры, зависит от природы тела и состояния его поверхности. Эти факторы можно учесть, если в формулу (19) ввести коэффициент 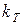 , показывающий, во сколько раз энергетическая светимость абсолютно чёрного тела при данной температуре больше энергетической светимости реального тела при той же температуре
, показывающий, во сколько раз энергетическая светимость абсолютно чёрного тела при данной температуре больше энергетической светимости реального тела при той же температуре
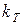 =
= 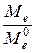 , (20)
, (20)
откуда 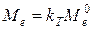 , или
, или 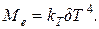 (21)
(21)
Для всех реальных тел 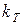 <1 и зависит как от природы тела и состояния его поверхности, так и от температуры. В частности, для вольфрамовых нитей электроламп накаливания зависимость
<1 и зависит как от природы тела и состояния его поверхности, так и от температуры. В частности, для вольфрамовых нитей электроламп накаливания зависимость 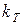 от Т имеет вид, представленный на рис. 4.
от Т имеет вид, представленный на рис. 4.
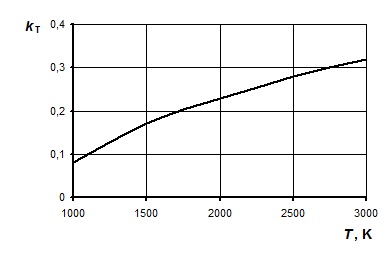
Рис. 4
Измерение энергии излучения и температуры электропечи основано на эффекте Зеебека, заключающемся в возникновении электродвижущей силы в электрической цепи, состоящей из нескольких разнородных проводников, контакты которых имеют различную температуру.
Два разнородных проводника образуют термопару, а последовательно соединенные термопары – термостолбик. Если контакты (обычно спаи) проводников находятся при различных температурах, то в замкнутой цепи, включающей термопары, возникает термоЭДС, величина которой однозначно определяется разностью температур горячих и холодных контактов, количеством последовательно соединенных термопар и природой материалов проводников.
Величина термоЭДС, возникающей в цепи за счет энергии падающего на спаи термостолбика излучения, измеряется милливольтметром, размещенным на передней панели измерительного устройства. Шкала этого прибора проградуирована в милливольтах.
Температура абсолютно черного тела (печи) измеряется с помощью термоэлектрического термометра, состоящего из одной термопары. Её ЭДС измеряется милливольтметром, также расположенным на передней панели измерительного устройства и проградуированным в °С.
Примечание. Милливольтметр фиксирует разность температур горячего и холодного спаев термопары, поэтому для получения температуры печи необходимо к показанию прибора прибавить значение температуры в помещении.
В данной работе проводят измерение термоЭДС термостолбика, величина которой пропорциональна энергии, затраченной на нагревание одного из контактов каждой термопары столбика, и, следовательно, энергетической светимости (при равных интервалах времени между измерениями и неизменной площади излучателя):
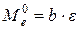 , (22)
, (22)
где b – коэффициент пропорциональности.
Приравнивая правые части равенств (19) и (22), получаем:
s×Т4=b×e,
откуда 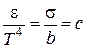 ,
,
где с – постоянная величина.
Одновременно с измерением термоЭДС термостолбика измеряют разность температур Δt горячего и холодного спаев термопары, помещенной в электропечь, и определяют температуру печи.
Используя экспериментально полученные значения температуры абсолютно черного тела (печи) и соответствующие им значения термоЭДС термостолбика, определяют значение коэффициента пропорционально-
сти с 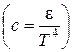 , которое во всех опытах должно быть одинаковым. Затем строят график зависимости с= f(Т), который должен иметь вид прямой, параллельной оси температур.
, которое во всех опытах должно быть одинаковым. Затем строят график зависимости с= f(Т), который должен иметь вид прямой, параллельной оси температур.
Таким образом, в лабораторной работе устанавливаетсяхарактер зависимости энергетической светимости абсолютно черного тела от его температуры, т.е. проверяется закон Стефана–Больцмана.
Дата добавления: 2016-10-07; просмотров: 2502;











