Определение перемещений энергетическими методами.
Рассмотренные выше методы неприменимы для балок с криволинейной осью и для рам. Более универсальными в этом смысле являются энергетические методы. Наиболее популярным является метод Мора (интеграл Мора).
Согласно методу Мора рассматриваются два состояния системы (балки, рамы): грузовое и единичное.
Грузовое состояниеобусловлено действием на систему заданной внешней нагрузки. Возникающие при этом силовые факторы и их эпюры называются грузовыми.
Единичное состояниеобусловлено действием на систему единичной обобщённой нагрузки, приложенной по направлению искомого перемещения. Возникающие при этом силовые факторы и их эпюры называются единичными. Под обобщённой нагрузкой понимается либо сосредоточенная сила, либо сосредоточенный момент. Обобщённой нагрузке соответствуют обобщённые перемещения.Сосредоточенной силе соответствует линейное перемещение. Сосредоточенному моменту соответствует угол поворота сечения.
Пренебрегая перемещениями, связанными с деформацией сдвига ввиду их малости по сравнению с деформацией изгиба интеграл Мора для случая прямого плоского изгиба запишется в виде:
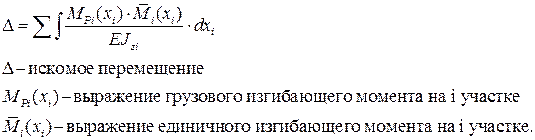
Во всех энергетических методах знак результата означает:
Знак « + » - искомое перемещение совпадает по направлению с приложенной единичной нагрузкой.
Знак «-» - искомое перемещение противоположно по направлению приложенной единичной нагрузке.
Графический способ вычисления интеграла Мора – способ Верещагина.
Формула Верещагина записывается в виде:
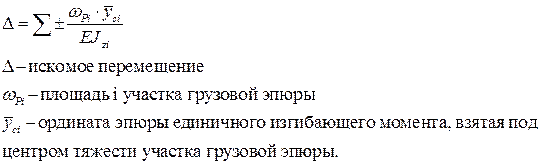
Знак « + » - когда площадь грузовой эпюры совпадает по направлению с эпюрой от единичной нагрузки.
Знак «-» - когда площадь грузовой эпюры противоположна по направлению эпюре от единичной нагрузки.
Минимальное количество слагаемых в формуле Верещагина равно количеству участков эпюры единичного момента. Если границы эпюры грузового момента не совпадают с границами эпюры единичного момента, то грузовую эпюру необходимо дополнительно разбить по границе единичной эпюры.
Если имеются трудности с определением площадей и положений центров тяжести участков грузовых эпюр, то для вычисления интеграла Мора
Рационально использовать формулу Симпсона-Корнаухова:
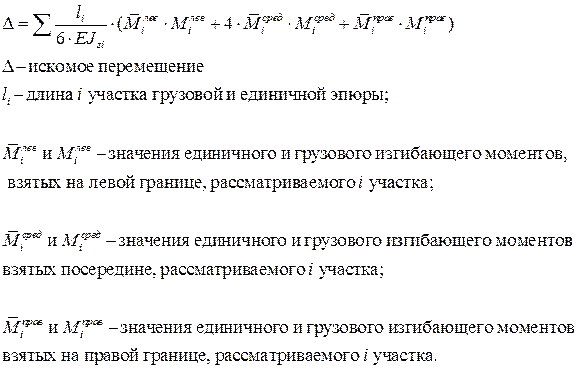
Формула Симпсона - Корнаухова справедлива для конструкций с прямыми участками (для балок и рам). Грузовая эпюра должна быть линейна или является параболой не выше второй степени.
Отметим, что перемещения, определённые с помощью дифференциального уравнения изогнутой линии балки и с помощью энергетического метода получаются одинаковыми по абсолютной величине.
Для оценки величины полученной деформации вычисляют значение перемещения 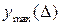 балки. Значения
балки. Значения 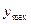 приведены в учебниках по сопротивлению материалов для различных случаев нагружения балок.
приведены в учебниках по сопротивлению материалов для различных случаев нагружения балок.
Величина прогиба нужна для проверки условия жёсткости: максимальный прогиб не должен превышать допускаемого. Можно воспользоваться значением 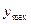 из справочника при вычислении значения приложенных нагрузок.
из справочника при вычислении значения приложенных нагрузок.
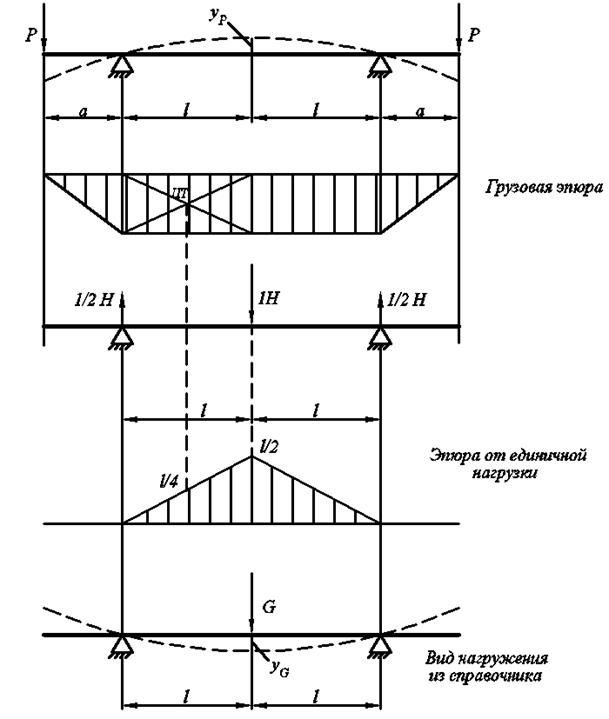
Пример: Вычислим значение реакции средней опоры для двухпролётной неразрезной балки с консолями, где
l – длина пролёта;
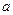 – длина консоли;
– длина консоли;
Р – нагрузка.
Для вычисления величины прогиба 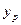 от сил Р воспользуемся методом Верещагина. Для этого нужно площадь грузовой опоры умножить на значение реакции средней опоры для двухпролётной неразрезной балки с консолями. Для вычисления величины прогиба
от сил Р воспользуемся методом Верещагина. Для этого нужно площадь грузовой опоры умножить на значение реакции средней опоры для двухпролётной неразрезной балки с консолями. Для вычисления величины прогиба 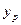 от сил Р воспользуемся методом Верещагина. Для этого нужно площадь грузовой опоры умножить на значение реакции средней опоры для двухпролётной неразрезной балки с консолями.
от сил Р воспользуемся методом Верещагина. Для этого нужно площадь грузовой опоры умножить на значение реакции средней опоры для двухпролётной неразрезной балки с консолями.
Для вычисления величины прогиба 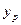 от сил Р воспользуемся методом Верещагина:
от сил Р воспользуемся методом Верещагина:
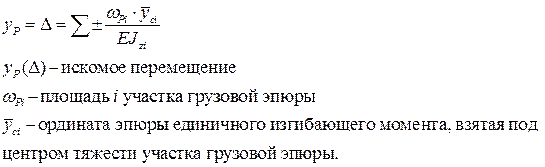
Для этого нужно площадь грузовой эпюры умножить на ординату эпюры от единичной нагрузки, находящуюся на одной линии с центром тяжести площади грузовой эпюры, получаем:
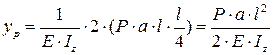 ,
,
где 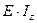 – жёсткость сечения.
– жёсткость сечения.
Значение величины прогиба 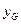 , возникающее от действия силы
, возникающее от действия силы 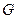 , приложенной в середине, возьмём из справочника по сопротивлению материалов:
, приложенной в середине, возьмём из справочника по сопротивлению материалов:
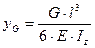 .
.
Приравнивая величины прогибов 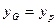 ,
,
получим: 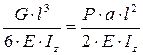 , следовательно:
, следовательно: 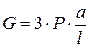
Дата добавления: 2021-01-11; просмотров: 546;











