Сдвиг порогового напряжения вследствие квантового эффекта

При комнатной температуре и 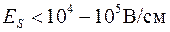величины самого низкого энергетического уровня 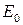и расстояния между подзонами сравнимы или меньше, чем 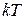. Поэтому большое число подзон занято. В этом случае 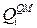в сущности такое же, как классическая плотность инверсного заряда на единицу площади, даваемая выражением (2.4.7) в лекции 2:

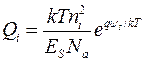. (9.4.1)

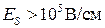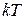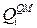Однако, когда , расстояние между подзонами становится больше, чем , и становится значительно меньше, чем 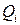. Сравнение квантовомеханической зависимости 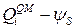(выражение (9.3.3))с классической кривой 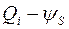(выражение (9.4.1)) на полулогарифмической шкале, показывает, что требуется дополнительный изгиб зон, чтобы достичь того же самого инверсного заряда на единицу площади как в классическом случае. Классическое условие порога, 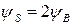, поэтому должно измениться на 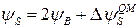, так, чтобы выполнялось условие

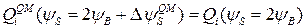. (9.4.2) Величину квантового сдвига 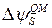можно оценить исходя из предположения, что только самая нижняя подзона (дважды вырожденная, 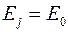) занята электронами, что справедливо при 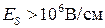. В этом случае выражение (9.4.2) с учетом (9.3.3) и (9.4.1) принимает вид (учитывается только основное состояние):

,

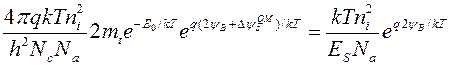откуда

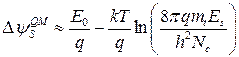. (9.4.3)

Рис 9.6 демонстрирует расчетное значение 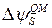как функцию 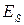. Зависимость (9.3.3) представлена на рис.9.6 пунктирной кривой.

Зная 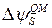, можно легко рассчитать сдвиг порогового напряжения вследствие квантового эффекта (смотри выражение (3.1.2а)):

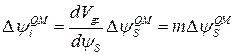, (9.4.4)

где 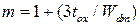как и ранее.

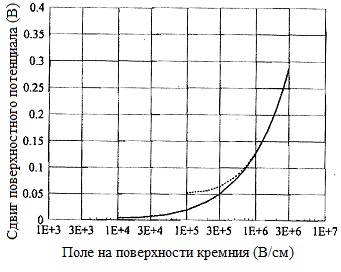
Рис.9.6. Дополнительный изгиб зон 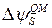(сверх классического 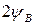), требуемый для достижения условия порога, как функция электрического поля на поверхности. Пунктирная кривая рассчитана при сохранении только наименьшего члена (дважды вырожденного) в выражении (9.3.3) [1].