Плотность квантовомеханического инверсного заряда
Рис. 9.5 показывает энергетическую диаграмму квантованного инверсного слоя на поверхности кремния, где дно зоны проводимости с энергией 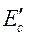 ниже, чем дно зоны проводимости в объеме
ниже, чем дно зоны проводимости в объеме  на величину
на величину 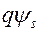 (изгиб зоны) вследствие приложенного поля затвора. Для j-той подзоны минимальная энергия, отсчитываемая от
(изгиб зоны) вследствие приложенного поля затвора. Для j-той подзоны минимальная энергия, отсчитываемая от 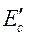 , равна
, равна
 . (9.3.1) (9.3.1)
. (9.3.1) (9.3.1)
Суммируя по всем подзонам в обеих долинах и используя (9.2.5), получаем полную плотность инверсного заряда на единицу площади:
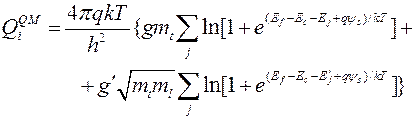 . (9.3.2)
. (9.3.2)
Заметим, что для первой группы подзон в выражении (9.3.2) ограничение по направлению х действует в продольном направлении, и эффективная масса плотности состояний 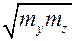 есть
есть 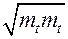 или
или  . Для второй подгруппы подзон в выражении (9.3.2) ограничение по направлению х перпендикулярно к продольному направлению, и эффективная масса плотности состояний
. Для второй подгруппы подзон в выражении (9.3.2) ограничение по направлению х перпендикулярно к продольному направлению, и эффективная масса плотности состояний 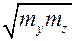 есть
есть  . В подпороговой области уровень Ферми по меньшей мере на несколько
. В подпороговой области уровень Ферми по меньшей мере на несколько  ниже самой низкой энергии подзоны
ниже самой низкой энергии подзоны 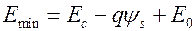 , и коэффициент
, и коэффициент 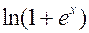 может быть аппроксимирован
может быть аппроксимирован 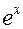 в обоих членах выражения (9.3.2). Поскольку
в обоих членах выражения (9.3.2). Поскольку  и
и  есть равновесная концентрация электронов в объеме кремния, выражение (9.3.2) упрощается
есть равновесная концентрация электронов в объеме кремния, выражение (9.3.2) упрощается
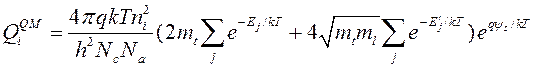 , (9.3.3)
, (9.3.3)
где подставлены 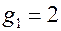 и
и 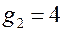 .
.
Дата добавления: 2018-05-25; просмотров: 721;











