Плотность состояний 2D электронного газа

Получим выражения для плотности состояний и плотности инверсного заряда 2D электронного газа в плоскости (у,о,z).

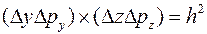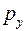Согласно квантовой механике объем одного разрешенного состояния в двухмерном фазовом пространстве координат-квазиимпульсов составляет , где и 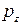− компоненты квазиимпульса электрона и h – постоянная Планка. Если 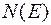– число состояний в единичном интервале энергий (плотность состояний), то 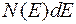− число состояний электрона с энергией между 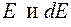на единицу площади, тогда

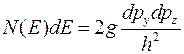, (9.2.1) где 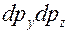− площадь в пространстве импульсов, внутри которой лежит энергия электронов между 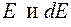, g – фактор вырождения подзоны и коэффициент 2 возникает из-за двух возможных направлений спина электрона.

Если 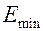− энергия основного состояния определенной подзоны, закон дисперсии вблизи дна этой подзоны имеет вид

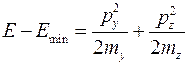, (9.2.2)

где 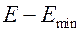− кинетическая энергия электрона, 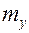и 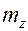− эффективные массы. Площадь эллипса, определяемая (9.2.2) в пространстве квазиимпульсов, равна 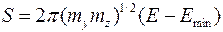. Следовательно, площадь 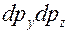, внутри которой энергия электрона находится между 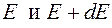, равна 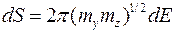, и (9.2.1) записывается в виде

.

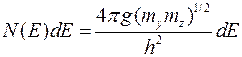Таким образом, плотность состояний двумерного электронного газа не зависит от энергии:

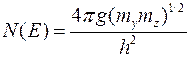. (9.2.3)

Число электронов на единицу площади в этой подзоне равно

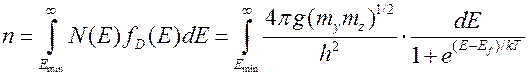, (9.2.4)

где 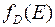− функция распределения Ферми-Дирака. Так как 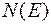− константа и может быть вынесена из-под знака интеграла, выражение (9.2.4) может быть легко проинтегрировано, что дает

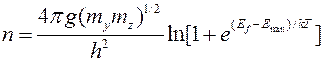. (9.2.5)

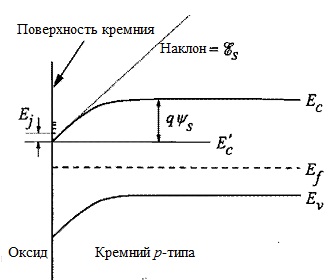Рис. 9.5 .[1]