Симметрия в уравнениях
Когда кригинг начинал развиваться, компьютерное оборудование было бедным. Обращение больших матриц для решения больших наборов линейных уравнений требовало очень много времени. Это стимулировало геостатистиков искать пути сокращения размера систем кригинга. Один из них - принимать во внимание симметрию системы. Например, данное в предыдущей главе упражнение рассматривало обычный кригинг блока, используя 5 точек данных, четыре из которых размещались симметрично вне блока. Для этих точек факторы взвешивания явно идентичны.
*Z2

*Z3 *Z1 *Z5
*Z4
Рис 8.8. Конфигурация с симметричными данными
Эти четыре пробы можно перегруппировать и рассматривать, как одну S с единственным фактором взвешивания. Каждая из исходных индивидуальных проб будет ее одной четвертью. Если первый вес связан с центральной точкой Z1, а второй вес с группой S, то систему кригинга можно переписать, как:
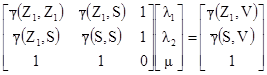 [8.1]
[8.1]
Поскольку не является очевидным, как вычислять различные вариограммные величины, то это будет представлено в подробностях.
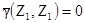 ,
, 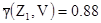 [8.2]
[8.2]
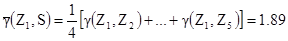 [8.3]
[8.3]
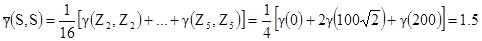 [8.4]
[8.4]
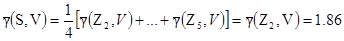 [8.5]
[8.5]
Это приводит к решению системы 3 на 3 вместо 6 на 6:
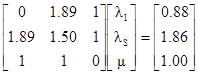 [8.6]
[8.6]
Решением является l1=0.60, lS=0.40 и m=0.12 и поэтому:
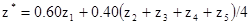 [8.7]
[8.7]
Конечно 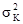 будет такая же, как и раньше. Здесь мы преуспели в сокращении системы от 6 на 6 до 3 на 3 без какой-либо потери точности. Так как время, необходимое для обращения матрицы, грубо пропорционально кубу размера системы, то уменьшая в два раза размер системы, мы эффективно уменьшаем время и, следовательно, стоимость вычислений на величину примерно равную одной восьмой от их первоначальных значений. Это конечно представляет значительную экономию.
будет такая же, как и раньше. Здесь мы преуспели в сокращении системы от 6 на 6 до 3 на 3 без какой-либо потери точности. Так как время, необходимое для обращения матрицы, грубо пропорционально кубу размера системы, то уменьшая в два раза размер системы, мы эффективно уменьшаем время и, следовательно, стоимость вычислений на величину примерно равную одной восьмой от их первоначальных значений. Это конечно представляет значительную экономию.
Понимая, что размер системы кригинга может быть значительно уменьшен (в некоторых случаях без потери точности), важно уметь отличать симметричную конфигурацию проб от тех случаев, которые только кажутся симметричными на первый взгляд. Чтобы иметь идентичные веса точки данных должны быть симметричными относительно друг друга и относительно оцениваемых точки или блока. В приведенной ниже конфигурации точки данных симметричны относительно друг друга, но не относительно блока.
*Z2

*Z3 *Z1 *Z5
*Z4
Рис 8.9. Конфигурация симметричных данных с удаленным блоком
Другой случай, который часто ведет к ошибкам, связан с ситуацией, когда данные и блок симметричны относительно друг друга, но модель вариограммы анизотропная.
Предположим, что конфигурация данных такая же, как на Рис. 8.10, но модель вариограммы имеет зону 500м в СЮ направлении и - 250м в ВЗ направлении. После соответствующей корректировки измерения в ВЗ направлении становятся в два раза больше измерений в СЮ направлении. В итоге веса для Z3 и Z5 идентичны, как и для Z2 и Z4, но они не равны как раньше. Это обстоятельство должно быть учтено при перегруппировке точек данных.
*Z2 *Z2
 |  |
*Z3 *Z1 *Z5 *Z3 *Z1 *Z5
*Z4 *Z4
Рис 8.10. Конфигурация проб до и после принятия во внимание анизотропии
Дата добавления: 2019-05-21; просмотров: 861;











