Перекрестная проверка

Так как к экспериментальной вариограмме могут быть подогнаны несколько различных моделей вариограмм, то хорошо было бы знать, какая из них "лучшая". Часто для этого используется перекрестная проверка (кроссвалидейшн). Процедура состоит во временном удалении одной точки данных из исходного набора и оценки ее кригингом, используя оставшиеся пробы. Если эту операцию повторить для всех точек (или для созданного подмножества их) и для всех подобранных моделей вариограмм, то мы получим серию ошибок оценивания для каждой точки данных и для каждой модели вариограммы. Когда вариограмма подходит к данным, то среднее ошибок оценивания и среднее стандартизованных ошибок оценивания должны быть равны нулю, а дисперсия стандартизованных ошибок оценивания должна равняться 1.0.

Пусть 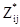обозначает кригинговую оценку i-ой точки, вычисленной с использованием j-ой модели вариограммы, и пусть 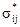- дисперсия кригинга. Если действительное значение в точке - Z_i, то соответствующая ошибка оценивания будет – 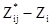. Поэтому мы можем записать:

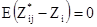[8.10]

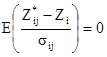[8.11]

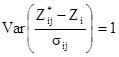[8.12]

Это приводит нас к вычислению следующих статистик:

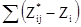[8.13]

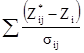[8.14]

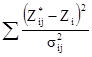[8.15]

Так как любые крайние значения (т.е. выбросы) сильно действуют на все эти статистики, то было бы предпочтительно использовать их надежные (робастные) формы. Но не важно используются ли надежные или ординарные статистики, потому, что все три статистики никогда не показажут одну и ту же модель, как "лучшую". Поэтому должен быть сделан выбор.

Существуют практические проблемы в использовании этой методологии с данными бурения, потому что, когда выбирается и оценивается проба, то результат кригинговой оценки зависит в основном от ближайших проб (т.е. тех, которые выше и ниже по вертикали). Поэтому данная перекрестная проверка проверяет только, насколько хорошо подогнан вертикальный компонент вариограммной модели, а не вся оставшаяся модель.