Проверка качества конфигурации кригинга

Наблюдая, как веса и дисперсия кригинга изменяются при увеличении числа точек, мы получаем некоторое понимание о том, что размер окрестности кригинга может быть оптимальным. Опыт показал, что дисперсия кригинга является довольно нечувствительным параметром для проверки качества конфигурации кригинга. Вес среднего в простом кригинге и наклон линейной регрессии истинного значения и оценки оказываются гораздо более чувствительными параметрами контроля качества и, следовательно, более полезными. Теорема аддитивности в Главе 7 доказала, что оценку ОК можно записать как

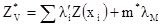[8.8]

где m* - кригинговая оценка среднего, и что дисперсия ОК может быть представлена суммой дисперсии SK и выражением, зависящим от веса среднего в SK и дисперсии кригинга оценки среднего:

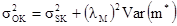[8.9]

Первое уравнение показывает, что там, где вес среднего в простом кригинге l_M мал (около 0), оценка в основном будет зависеть от локальных значений Z(x), т.е. от данных из конфигурации кригинга, а не от оценки m. Поэтому степень требуемой стационарности становится меньше. К тому же ОК оценка и SK оценка являются близкими друг к другу.

Второе уравнение показывает, что когда вес среднего в SK мал, то дисперсия OK близка к SK дисперсии. При этом слегка теряется точность при оценивании среднего. Наоборот, когда вес среднего в SK большой, то дисперсия OK становится больше чем дисперсия SK. Rivoirard (1984, 1987) показал, что уменьшение информации, доступной в окрестности кригинга, увеличивает важность среднего. Поэтому этот параметр показывает, как разброс данных связан с моделью вариограммы и также – какой уровень стационарности данных будет достаточным.