Зеркально-поворотная симметрия

Операция поворота тела вокруг неподвижной оси на угол 360^°/n с последующим отражением его в плоскости, перпендикулярной к той же оси, называется зеркально-поворотным преобразованием. Если в результате такого преобразования тело переходит само в себя, то соответствующую ось называют зеркально-поворотной осью n-го порядка и обозначают символом S_n.

На рис. 4.9 изображена система из четырех точек ABCD, которая обладает зеркально-поворотной осью четвертого порядка. Очевидно, эта ось является также обычной поворотной осью второго порядка.

Можно доказать, что при нечетном n зеркально-поворотная ось n-го порядка не является новым элементом симметрии, а сводится к комбинации поворотной оси n-го порядка С_n и перпендикулярной к ней плоскости симметрии σ_h. Поэтому при рассмотрении зеркально-поворотных осей достаточно ограничиться осями четных порядков.

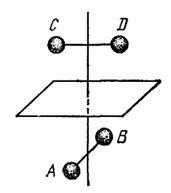
	Рис. 4.9. Система из четырех точек ABCD, которая обладает зеркально-поворотной осью четвертого порядка. Эта ось является также обычной поворотной осью второго порядка.
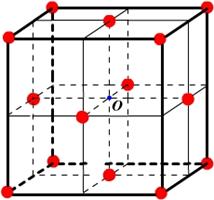
Рис. 4.10. Один из центров симметрии (О) ГЦК решетки.

Множество всех зеркально-поворотных преобразований, которые переводят кристаллическую решетку в себя называется группой зеркально-поворотных преобразований кристалла. Симметрию кристалла по отношению к этим преобразованиям называют зеркально-поворотной симметрией.