Коды для представления чисел в компьютере

Взаимно однозначное преобразование слов называется кодированием. В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. При помощи этих кодов упрощается определение знака результата операции. Операция вычитания (или алгебраического сложения) чисел сводится к арифметическому сложению кодов, облегчается выработка признаков переполнения разрядной сетки. В результате упрощаются устройства ЭВМ, выполняющие арифметические операции. Для представления чисел со знаком в ЭВМ применяют прямой, обратный и дополнительный коды.

Общая идея построения кодов такова. Код трактуется как число без знака, а диапазон представляемых кодами чисел без знака разбивается на два поддиапазона. Один из них представляет положительные числа, а другой – отрицательные. Разбиение выполняется таким образом, чтобы принадлежность к поддиапазону определялась максимально просто. Очень удобно формировать коды так, чтобы значение старшего разряда указывало на знак представляемых чисел. Использование такого кодирования позволяет говорить о старшем разряде как о знаковом, а об остальных – как о цифровых разрядах кода, хотя в общем случае код трактуется как число без знака.

Прямой код

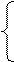Прямой код двоичного числа G, представляемого в n - разрядной сетке, определяется как

G , при G>=0;

G_пр= A+|G|, при G<=0,

где А – величина, равная весу старшего разряда сетки (для дробей А = 1, а для целых А = 2^n-1). Диапазон представляемых прямым кодом чисел 0<=|G|<A.

Признаком представления положительных (отрицательных) чисел является наличие 0 (1) в старшем разряде, называемом знаковым. Таким образом, положительные числа представляются кодами 0<=G_пр<A, а отрицательные A<=G_пр<2A.

Сложение в прямом коде чисел, имеющих одинаковые знаки, выполняется достаточно просто. Числа складываются, и сумме присваивается код знака слагаемых. Значительно более сложной является операция алгебраического сложения в прямом коде чисел с разными знаками. В этом случае приходится определять большее по модулю число, производить вычитание чисел и присваивать разности знак большего по модулю числа.

Операция вычитания (алгебраического сложения) сводится к операции простого арифметического сложения при помощи обратного и дополнительного кодов, используемых для представления в ЭВМ чисел со знаком.

Обратный код

Обратный код двоичного числа G, представляемого в n - разрядной сетке, определяется как

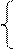
G , при G>=0;

G_обр= В-|G| , при G<=0,

где В – величина наибольшего числа без знака, размещающегося в n - разрядной сетке (для дробей В=2-2^-(n-1), а для целых В=2ⁿ-1). Диапазон представляемых обратным кодом чисел такой же, как и у прямых кодов: 0<= |G| <A. По определению обратный код отрицательного числа представляет собой дополнение модуля исходного числа до наибольшего числа без знака, помещающегося в разрядную сетку. В связи с этим получение обратного кода двоичного отрицательного числа сводится к получению инверсии n - разрядного кода модуля этого числа. Т.к. модуль чисел, представимых в n - разрядной сетке, |G|<A, в старшем (знаковом) разряде обратного кода у положительных чисел будет 0, а у отрицательных 1. В цифровых разрядах обратного двоичного кода представляется либо модуль числа (для положительных чисел), либо его инверсия (для отрицательных чисел).

Дополнительный код

Дополнительный код двоичного числа G, представляемого в n - разрядной сетке, определяется как

G , при G>=0;

G_доп = С - |G|, при G<0,

где С – величина, равная весу разряда, следующего за старшим разрядом используемой разрядной сетки (для дробей С=2, а для целых чисел С=2ⁿ). Диапазон представляемых дополнительным кодом чисел отличается от диапазона прямого или обратного кода. Для положительных и отрицательных чисел поддиапазоны различны. Для положительных чисел (как и у прямого кода) 0<=G<A, а для отрицательных 0<|G|<=A. Из определения дополнительного кода следует, что старший (знаковый) разряд у кода положительного числа равен 0, а у кода отрицательного числа 1. В цифровых разрядах дополнительного кода положительного числа представляется модуль этого числа. Дополнительный код отрицательного числа удобно получать через обратный код.

Если рассматривать обратный и дополнительный коды числа как двоичные числа без знаков, то для отрицательных двоичных дробей G_доп=G_обр+2^-(n-1), а для отрицательных двоичных целых чисел G_доп=G_обр+1.

Таким образом, дополнительный код отрицательного числа может быть получен из обратного путем прибавления 1 к младшему разряду обратного кода.

При выполнении расчетов на ЭВМ может возникнуть как "положительный", так и "отрицательный" ноль. Положительный ноль в прямом, дополнительном и обратном кодах имеет вид:

(+0)пр=000...0;

(+0)доп=000...0;

(+0)обр=000...0.

Отрицательный ноль изображается

в прямом коде

(-0)пр=100...0,

в обратном коде

(-0)обр=111...1,

в дополнительном коде отрицательный ноль отсутствует.

При представлении чисел дополнительным кодом ноль имеет единственное изображение. При применении обратного кода "положительный" и "отрицательный" ноль имеют разные изображения. Изменение знака числа, представленного в прямом коде, выполняется инвертированием его знакового разряда.

Изменению знака числа соответствует инвертирование его кода, если число представлено в обратном коде, и инвертирование и добавление 1 к младшему разряду, если число представлено в дополнительном коде.

Рассмотрим применение обратного и дополнительного кодов при алгебраическом сложении n - разрядных двоичных чисел G и Q. Могут быть сформулированы следующие правила (предполагаем, что модуль алгебраической суммы меньше 1 для дробей и меньше 2^n-1 для целых, и, следовательно, код суммы представим в n - разрядной сетке).

При алгебраическом сложении двух двоичных чисел, представленных обратным (или дополнительным) кодом, производится арифметическое суммирование этих кодов, включая разряды знаков. При возникновении переноса из разряда знака единица переноса прибавляется к младшему разряду суммы кодов (такой перенос называется круговым или циклическим) при использовании обратного кода и отбрасывается при использовании дополнительного кода. В результате получается алгебраическая сумма в обратном (дополнительном) коде.

Пример.

Разрядная сетка n=8. Сложить в обратном коде -3 и -7.

Число (7)₁₀ = (00000111)₂ (-7)обр= 11111000;

число (3)₁₀ = (00000011)₂ (-3)обр=11111100;

складываем

11111000

+11111100

+ 1

11110101 (обратный код суммы)

Для проверки правильности вычисления инвертируем полученный код и получим код 00001010. Это соответствует (10)₁₀. Получили число, равное сумме с противоположным знаком.

При алгебраическом сложении двух чисел, помещающихся в разрядную сетку, может возникнуть переполнение, т.е. может образоваться сумма, требующая для своего представления на один цифровой разряд больше по сравнению с разрядной сеткой слагаемых.

Правило (признак) переполнения разрядной сетки.

При алгебраическом сложении двух двоичных чисел с использованием дополнительного (обратного) кода для их представления признаком переполнения является наличие переноса в знаковый разряд суммы при отсутствии переноса из ее знакового разряда (положительное переполнение) или наоборот (отрицательное переполнение). Если и в знаковый, и из знакового разряда суммы есть переносы или нет этих переносов, то переполнение отсутствует. При положительном переполнении результат операции положительный, при отрицательном – отрицательный.

Смещенный код.

Помимо рассмотренных кодов для представления чисел со знаком применяется еще смещенный код. Этот код обычно используется для представления целых чисел, задающих порядки чисел с плавающей точкой. Определяется смещенный код двоичного числа G, представленного в n - разрядной сетке, как G_см=А+G, либо, что то же самое,

А+|G| , при G>=0;

Gсм= A - |G| , при G<0,

где А (смещение) – величина, равная весу старшего разряда сетки (для целых А=2^n-1). Диапазон представляемых чисел такой же, как и у дополнительного кода. Единица в знаковом разряде смещенного кода указывает на представление положительного числа, ноль – отрицательного.

Цифровые разряды смещенного кода для положительного числа представляют модуль этого числа, для отрицательного – инверсию модуля, к которой подсуммирована 1 к младшему разряду.

Существует простое правило перехода к смещенному коду от дополнительного (и наоборот): для перехода необходимо инвертировать знаковый разряд кода.

Важной особенностью смещенного кода является то, что из G1см>G2см следует G1>G2. Использование смещенных кодов упрощает сравнение чисел со знаком, сводя его к сравнению представляющих их чисел без знака (смещенных кодов).

Сложение смещенных кодов может выполняться в соответствии со следующим ниже утверждением.

Сумма смещенных кодов с инвертированным старшим (знаковым) разрядом дает смещенный код суммы, при этом признаком получения положительного (отрицательного) переполнения является наличие (отсутствие) переноса из знакового разряда суммы, имевшего до инверсии значение 1 (0).

Вычитание смещенных кодов сводится к сложению уменьшаемого и вычитаемого, представляемого с противоположным знаком. Изменение знака числа в смещенном коде выполняется так же, как и в дополнительном.