Подбор модели для вертикальной вариограммы

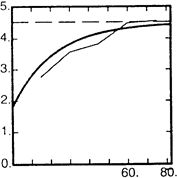
Теперь подгоним модель к полученной вертикальной вариограмме. Рисунок 5.3.a показывает, что она стабилизируется на высоте около 4.5 на расстоянии 65-70м, что дает нам значения порога и зоны влияния. Экстраполяция линии к началу дает эффект самородка около 2. Поэтому можно попробовать использовать эффект самородка 2.0 и либо сферическую модель с порогом 4.5 и зоной 65м, либо эквивалентную экспоненциальную модель. На Рисунке 5.4.a показано, что хорошей аппроксимацией является эффект самородка 1.8 и сферическая модель с зоной 65м и порогом 4.5, а наиболее близкая экспоненциальная модель подгоняется к экспериментальной функции значительно хуже (Рис. 5.4.a, b).

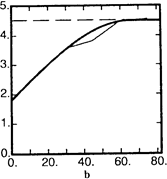
Рис 5.4. Две попытки подбора вертикальной вариограммы; b - сферическая модель с эффектом самородка 1.8, зоной 65м и порогом 4.5, и a - эквивалентная экспоненциальная модель.

Эта комбинация сферической модели и эффекта самородка не единственная, которая возможна в данном случае. Эффект самородка в принципе можно заменить любой структурой, у которой такой же порог и зона менее 15м. Проиллюстрируем это на Рис. 5.5, где сравнивается модель, состоящая их двух сферических с зонами 10м и 65м и порогами (составляющими порога) 1.8 и 2.7, с раннее подобранной сферической моделью. Конечно, возможно в первой структуре использовать другую величину эффекта самородка вместо нулевой.

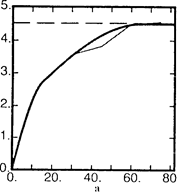
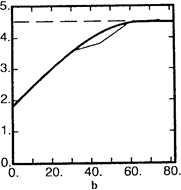
Рис 5.5.: Две модели, которые подгоняются к экспериментальной вариограмме; (a) две сферических структуры с зонами 10м и 65м, порогами 1.8 и 2.7 соответственно; (b) одна сферическая структура с эффектом самородка 1.8, зоной 65м и порогом 2.7