Вложение поля рациональных чисел в поле действительных чисел.

Договоримся обозначать поле действительных чисел через .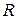

Теорема 3.Поле рациональных чисел вкладывается в поле действительных чисел.

Доказательство.

Рассмотрим множество 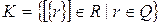. Нетрудно устанавливается, что 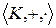подполе поля 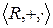, проверим только замкнутость.

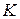замкнуто относительно сложения и умножения (?)

;

.

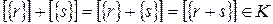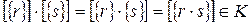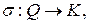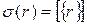
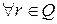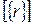Рассмотрим соответствие заданное по правилу , где - класс, порожденный постоянной последовательностью.

Докажем, что 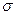- изоморфизм.

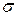- отображение (?)

Всюду определенность очевидна, поскольку для каждого рационального числа 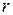можно построить класс .

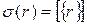Однозначность: (?)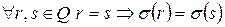

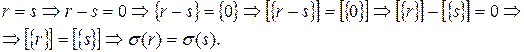
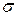- биекция (?)

Инъективность: (?)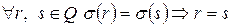

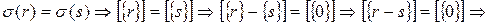
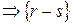- нулевая. Докажем равенство 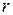и 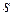методом от противного. Предположим, что 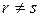. Возможны случаи:

1. .

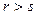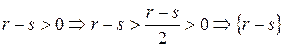- положительная.

2. 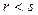аналогично.

- отрицательная.

Таким образом, в обоих случаях получено противоречие с условием 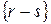- нулевая, а, значит .

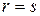Сюръективность: (?)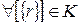

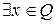
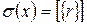Возьмем 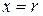, поскольку 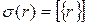. В силу произвольности 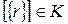сюръективность доказана.

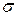- гомоморфизм (?)

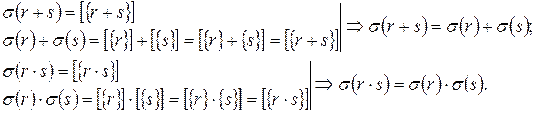
что и требовалось доказать.

Замечание 1. Ввиду изоморфизма, который отмечен в конце доказательства, мы проведем отождествление 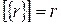для каждого рационального числа. Ввиду этого отождествления получим 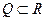(подмножество, более того, подполе).

Замечание 2. В одном классе лежат последовательности, имеющие одинаковые пределы.