Геометрическая интерпретация комплексного числа. Тригонометрическая форма записи комплексного числа.

Пусть .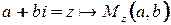

Каждому комплексному числу 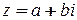ставится в соответствие точка 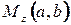в прямоугольной системе координат.

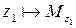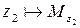Если и , то 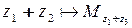. При этом .

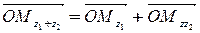Тригонометрическая форма записи комплексного числа возникает из геометрической интерпретации. Так, каждой точке 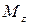можно поставить в соответствие радиус-вектор 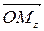, который определяется длиной 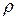и направлением – углом 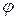отклонения от положительного направления оси .

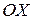Замечание. , , .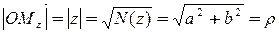

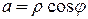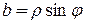Таким образом 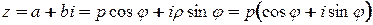. Последняя запись и есть тригонометрическая форма записи комплексного числа.

Предложение 2.Если 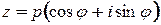, то 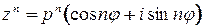для каждого .

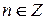Доказательство.

Пусть 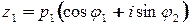, 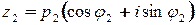. Тогда

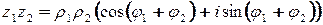. Последнее равенство и дает основание утверждать справедливость данной теоремы.

что и требовалось доказать.

Замечание. .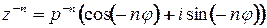

Корни - ой степени из единицы

Определение. Комплексное число 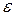называется корнем - ой степени из единицы, где 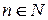, если .

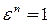Вычислим все корни - ой степени из единицы. Пусть 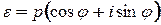. Зная, что 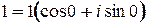, составим систему: 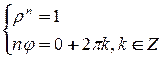. Тогда 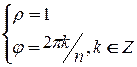и любой корень - ой степени из единицы будет иметь вид: .

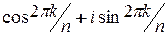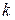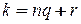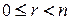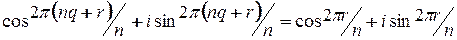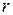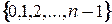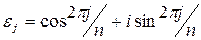Покажем, что существует ровно различных корней - ой степени из единицы. Для этого поделим на с остатком, получим , где . Следовательно, . Поскольку может принимать только одно из значений , то и различных корней - ой степени из единицы также будет ровно штук, причем , где .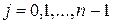

Теорема 3. Корни - ой степени из единицы образуют мультипликативную циклическую группу.

Доказательство.

Пусть 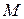- всех корней - ой степени из единицы. Очевидно, что 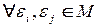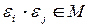. Тогда 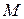замкнуто относительно умножения.

Операция умножения во множестве 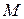ассоциативна; 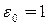- нейтральный элемент в ; .

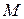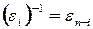Таким образом, 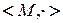группа, в которой элемент 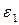является порождающим, так как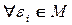 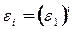, следовательно, 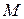- мультипликативная циклическая группа.

что и требовалось доказать.

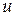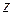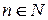Определение. Комплексное число называется корнем - ой степени из ненулевого комплексного числа , где , если .

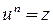Вычислим все корни - ой степени из комплексного числа 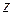. Пусть 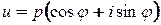, 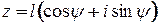. Зная, что 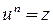, составим систему: 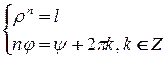. Тогда 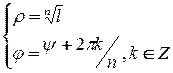и любой корень - ой степени из комплексного числа 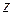будет иметь вид: .

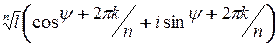Покажем, что существует ровно различных корней - ой степени из комплексного числа 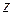. Для этого поделим 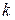на с остатком, получим 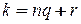, где 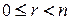. Следовательно,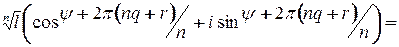

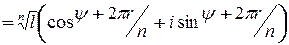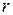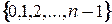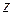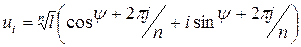. Поскольку может принимать только одно из значений , то и различных корней - ой степени из комплексного числа также будет ровно штук, причем , где .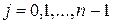

Замечание.Для каждого 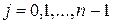справедливо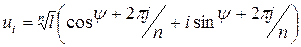

.

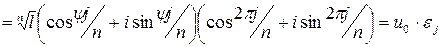Следствие.Все корни - ой степени из ненулевого комплексного числа 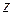являются результатом умножения одного из этих корней на корни - ой степени из единицы.

Пример. Найти все корни 3 – ей степени из -8.

Очевидно, что -2 – один из искомых корней. Тогда, согласно вышеприведенному следствию,

,

,

.

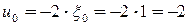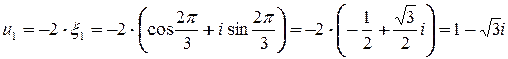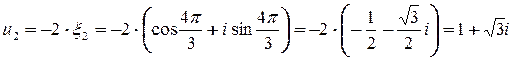Теорема 5.Полекомплексных чисел не является упорядоченным.

Доказательство.

Предположим, что 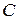упорядоченное поле с положительным конусом 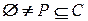. Согласно аксиомам положительного конуса, для элемента 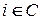справедливо одно из следующих условий:

1. 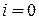, что противоречит ;

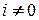2. 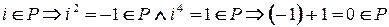, что противоречит ;

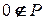3. 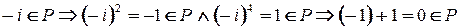, что противоречит .

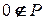Таким образом, ни одно из трех условий не выполняется, следовательно, предположение о существовании положительного конуса ложно, и, значит, 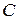не является упорядоченным полем.

что и требовалось доказать.

Лекция 11.

Тело кватернионов.

Открыл Уильям Роуан Гамильтон (ирландец) 1805-1865.

Определение. Ненулевое кольцо с единицей, в котором каждый элемент, отличный от нуля, обратим, называется телом.

Рассмотрим множество матриц:

,

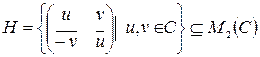где 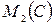- множество квадратных матриц с коэффициентами из поля комплексных чисел.

Теорема 1. 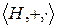тело.

Доказательство.

Покажем, что 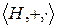- подкольцо кольца 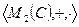, используя признак подкольца:

.

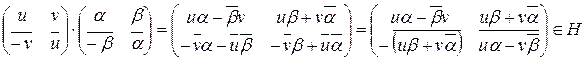
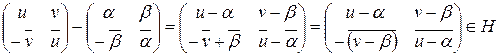- кольцо с единицей (?)

Элемент 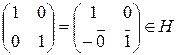является нейтральным элементом по сложению, поскольку .

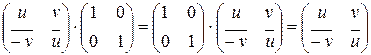Проверим, что любой ненулевой элемент кольца 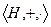обратим:

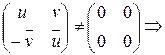
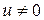или 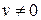. . 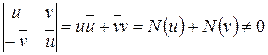Из последнего следует, что любая ненулевая матрица 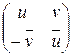невырожденная, следовательно, она обратима в кольце 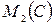. Найдем обратную:

.

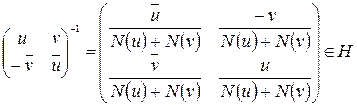что и требовалось доказать.

Определение. Тело 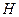назовем телом кватернионов, а его элементы кватернионами.

Теорема 2. Поле комплексных чисел изоморфно вкладывается в тело кватернионов.

Доказательство.

Рассмотрим соответствие 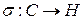, заданное по правилу .

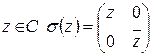Докажем, что 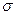- изоморфизм.

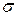- отображение (?)

Всюду определенность очевидна, поскольку для каждого комплексного числа 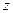можно построить матрицу .

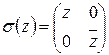Однозначность: (?)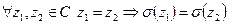

.

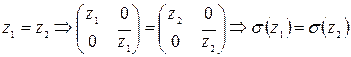- биекция (?)

Инъективность: (?)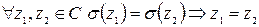

.

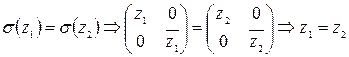Сюръективность: (?)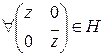

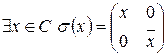Возьмем 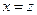, поскольку 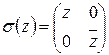. В силу произвольности 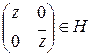сюръективность доказана.

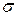- гомоморфизм (?)

.

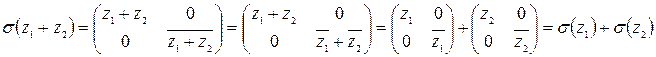
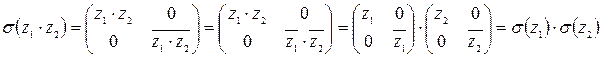что и требовалось доказать.

Замечание. Ввиду изоморфизма, который отмечен в конце доказательства, мы проведем отождествление кватерниона 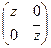с комплексным числом 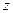. Ввиду этого отождествления получим 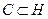(подмножество, более того, подтело).