Нулевые, положительные, отрицательные последовательности рациональных чисел.

Определение. Последовательность рациональных чисел, сходящаяся к 0, называется нулевой последовательностью.

Следствия из определения:

1. Любая нулевая последовательность рациональных чисел является ф.п.р.ч.

2. Любая подпоследовательность нулевой последовательности является нулевой.

3. Произведение, сумма и разность нулевых последовательностей является нулевой.

4. Множество всех нулевых последовательностей образует подкольцо в кольце всех ф.п.р.ч.

Определение. Последовательность рациональных чисел называется положительной, если .

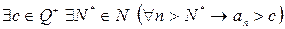Определение. Последовательность рациональных чисел называется отрицательной, если будет положительной.

Следствие.Любая подпоследовательность положительной (отрицательной) последовательности будет положительной.

Теорема 3.Сумма и произведение положительных последовательностей рациональных чисел является положительной последовательностью рациональных чисел.

Доказательство.

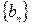Пусть и - положительные последовательности рациональных чисел, что влечет

.

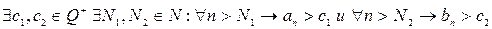Пусть 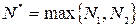. Тогда 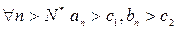. Последовательно складывая и умножая последние неравенства, получим 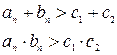. Поскольку , а 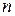- произвольное, большее 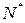число, последовательност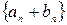и и 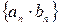положительны.

что и требовалось доказать

Теорема 4. Если фундаментальные последовательности и не являются положительными, тогда фундаментальная последовательность будет нулевой.

Доказательство.

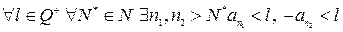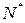По условию и не являются положительными, следовательно, . Учитывая фундаментальность последовательностей и , можно выбрать настолько большим, чтобы выполнялись неравенства:

Тогда

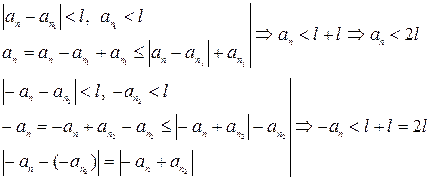
Выбрав 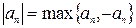, получим 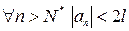для сколь угодно малого , а это возможно лишь в одном случае, если является нулевой последовательностью рациональных чисел.

что и требовалось доказать

Следствие.Если - ф.п.р.ч., тогда либо положительна, либо положительна, либо - нулевая.