Эквивалентные последовательности рациональных чисел

И их свойства.

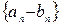Определение. Две фундаментальные последовательности рациональных чисел называются эквивалентными, если является нулевой последовательностью, иначе .

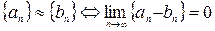Теорема 5.Отношение ≈ на множестве всех фундаментальных последовательностей рациональных чисел является отношением эквивалентности.

Доказательство.

Обозначим множество всех последовательностей рациональных чисел через .

1. Рефлективность (?)

.

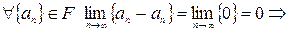
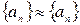2. Симметричность (?)

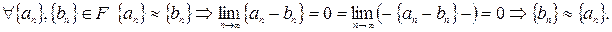3. Транзитивность (?)

.

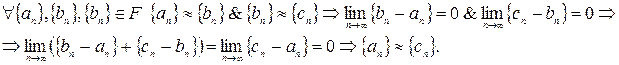что и требовалось доказать

Теорема 6. Любая подпоследовательность фундаментальной последовательности эквивалентна ей.

Доказательство.

Пусть - ф.п.р.ч., - произвольная подпоследовательность последовательности . Тогда 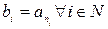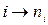- монотонно возрастающая функция на множестве натуральных чисел. Покажем, что .

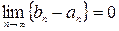В силу фундаментальности последовательности имеем 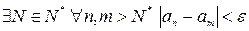. Учитывая это, получим

.

что и требовалось доказать

Теорема 7. Фундаментальная последовательность рациональных чисел, эквивалентная нулевой, положительной, отрицательной является соответственно нулевой, положительной, отрицательной.

Доказательство.

Пусть и 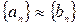. Тогда 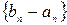- нулевая.

1. - нулевая.

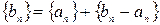- нулевая как сумма нулевых ф.п.р.ч.

2. - положительная.

Возьмем 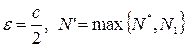. Тогда получим

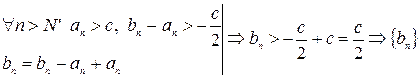- положительная.

3. 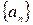- отрицательная.

Нетрудно проверяется, что 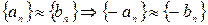. Тогда 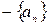- положительная, следовательно, согласно пункту 2 этой теоремы - положительная, а, значит, 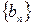- отрицательная ф.п.р.ч.

что и требовалось доказать

Теорема 8.Отношение ≈ стабильно относительно операции сложения, умножения и взятия противоположного на множестве всех фундаментальных последовательностей рациональных чисел.

Доказательство.

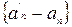Пусть . Тогда и 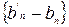- нулевые ф.п.р.ч.

Отношение ≈ стабильно относительно операции сложения (?)

Поскольку сумма нулевых последовательностей является нулевой, имеем 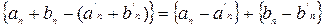- нулевая ф.п.р.ч., а значит .

Отношение ≈ стабильно относительно операции умножения (?)

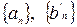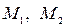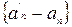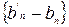Последовательности фундаментальные, следовательно, ограниченные, предположим, числами соответственно. Зная, что и нулевые ф.п.р.ч. имеем

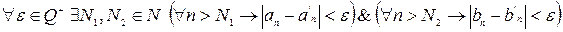. Выберем 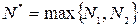. Тогда 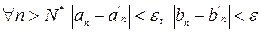. Принимая во внимание выше перечисленное, оценим

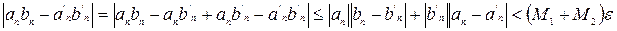. Последнее влечет, что 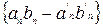является нулевой, а, значит, .

Отношение ≈ стабильно относительно операции взятия противоположного (?)

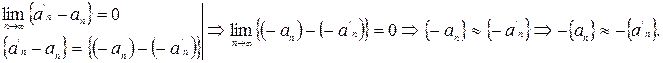что и требовалось доказать

Лекции 8-9.