Экспериментальные вариограммы

Содержание

Эта глава, как и предыдущая, посвящена вариограммам. Читатель узнает, как рассчитать экспериментальную вариограмму в одномерном, двухмерном и трехмерном пространствах, а также - как подобрать к ней модель. В конце приводится несколько примеров. Обсуждаются практические проблемы, встречающиеся в трудных случаях построения экспериментальными вариограммам. Они включают выбросы (outliers), почти регулярно распределенные данные, и так далее.

4.2 Как рассчитывать экспериментальные вариограммы:

Экспериментальную вариограмму можно вычислить, используя следующую формулу:

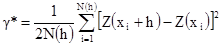[4.1]

где x_i – местоположение проб, Z(x_i) – их значения и N(h) – количество пар (x_i, x_i +h), разделенных расстоянием h, которые действительно используются в расчете. Эту формулу очень легко использовать, когда пробы регулярно расположены в одномерном пространстве, например вниз по скважине, вдоль подземной выработки или сейсмического профиля. Пример 1 иллюстрирует эту процедуру.

Если пробы не расположены по регулярной сети, то нельзя отсутствующие значения рассчитывать по соседним пробам или приравнивать нулю, потому что истинная изменчивость будет искажаться. Квадрат разности вычисляется для всех имеющихся пар проб.

Если данные не регулярны, то вариограммы вычисляются для классов расстояний с каким-либо связанным допуском, обычно 50%, потому что он перекрывает все возможные расстояния. Когда данные нерегулярно расположены в двухмерном пространстве, вариограммы рассчитываются как для классов расстояний, так и для углов (азимутов), характеризующих различные направления.

На плоскости

Когда данные двухмерные, вариограммы должны вычисляться по крайне мере в четырех направлениях для проверки анизотропии. Первый шаг – это выбор лага (lag) вариограммы и его допуск, затем – выбор основных углов и угловой допуск.

Процедура расчета реализуется следующим образом. На первом шаге для каждой точки программа подбирает все возможные пары с остальными точками и классифицирует их по установленным классам расстояний и направлений. Затем для каждой пары вычисляется квадрат разницы 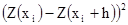, и результат добавляется к сумме соответствующего класса. Количество пар в классе также увеличивается на 1. Когда все возможные пары будут обработаны для точки x_i, программа перейдет к следующей точке. В конце процесса итоговые суммы делятся на 2 и на количество пар, которые были выбраны для данного класса. Блок-схема этого расчета приведена на Рис. 4.2.