Ранжирование альтернатив на множестве лингвистических векторных оценок

Задано множество альтернатив A == {а₁, а₂, ..., а_m} и множество соответствующих исходов S = [s₁, s₂, ..., s_m,}. Каждый исход s_j характеризуется альтернативой а_i и вектором лингвистических оценок на множестве критериев К = [К₁, К₂, .... К_n}. Множество лингвистических векторных оценок исходов К = {K(s₁), K(s₂), ..., K(s_m)} можно упорядочить, введя функцию принадлежности нечеткого отношения порядка m _³: К ´ К ® [0,1]. Для i-го критерия обозначим mⁱ _³ (K_i(s_j), K_i(s_k)) через mⁱ_³ (s_j , s_k) Значение этой функции можно вычислить по фоомуле

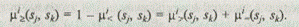
Степень истинности m < (s_j, s_k) нечеткого высказывания s_j < s_k можно определить как вероятность того, что точное значение s_j будет меньше точного значения s_k. Предполагая, что исходы являются независимыми случайными величинами, отношение m < (s_j, s_k) можно представить в виде:

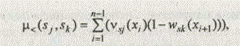
где v_s(x) — вероятность того, что в качестве точного значения нечеткого числа s используется величина х;

w_s(x) — вероятность того, что в качестве точного значения s используется величина у < х:

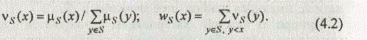
Векторные оценки могут быть упорядочены на основе функции принадлежности

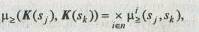
где х — обозначает символ обобщенной операции.

Так как между множеством альтернатив и исходив существует взаимно однозначное соответствие, функцию принадлежности нечеткого отношения предпочтения на множестве альтернатив можно представить в виде:

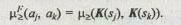
Решение задачи с использованием данного метода включает следующие основные шаги:

• вычисление функций принадлежности m_< с использованием соотношений (4.2);

• построение нечеткого отношения порядка m_³;

• минимизация отношения m_³;

• определение отношений предпочтения на множестве альтернатив и выявление лучшей альтернативы. Для этого вычисляется отношение предпочтения между альтернативой a_j и всеми остальными альтернативами, функция принадлежности которого имеет вид:

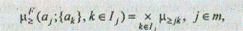
где I_j — множество индексов альтернатив, с которыми может сравниваться j-я альтернатива.

Решение задачи ранжирования можно описать соотношениями:

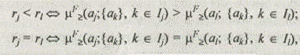
где r_j — ранг альтернативы.

Наиболее предпочтительная альтернатива имеет самый низкий ранг.