Основные теоремы теории вероятностей.
В таких сложных изделиях, какими являются, например, АД, возможны самые разнообразные виды отказов, и поэтому отказ АД должен рассматриваться как сложное событие, которое определяется совокупностью появления возможных отказов его агрегатов, узлов и систем. Причем отказы составных частей АД могут быть несовместными и независимыми событиями.
Сложное событие А, заключающееся в том, что произойдет либо событие А1, либо А2, либоАi либо Аn , называется суммой исходных событий и обозначается:
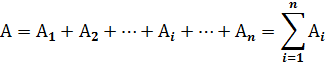
Пример: вынужденная посадка из-за отказа двигателя двухдвигательного ВС происходит в том случае, когда отказывает либо двигатель №1, либо двигатель №2, либо оба двигателя:
А(вынужденная посадка)= А1+А2
Сложное событие А, заключающееся в одновременном осуществлении нескольких событий, называется произведением исходных событий Аi и обозначается:
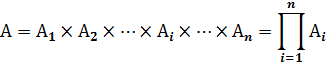
Пример: вынужденная посадка происходит в случае отказа обоих двигателей двухдвигательного ВС:
А(вынужденная посадка)= А1×А2
При определении вероятностей часто приходится образовывать сложные события в виде комбинаций более простых событий, применяя операции сложения и умножения.
Пример: имеется трехдвигательное ВС. Образуем событие, в котором откажет один двигатель.
А1 – 1й двигатель исправен; 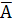 1 - 1й двигатель отказал;
1 - 1й двигатель отказал;
А2 – 2й двигатель исправен; 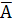 2 – 2й двигатель отказал;
2 – 2й двигатель отказал;
А3 – 3й двигатель исправен; 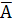 3 – 3й двигатель отказал;
3 – 3й двигатель отказал;
А= 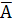 1× А2× А3+ А1×
1× А2× А3+ А1× 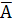 2×А3+ А1× А2×
2×А3+ А1× А2× 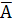 3
3
Сумму и произведение случайных событий можно показать с помощью диаграммы Венна:
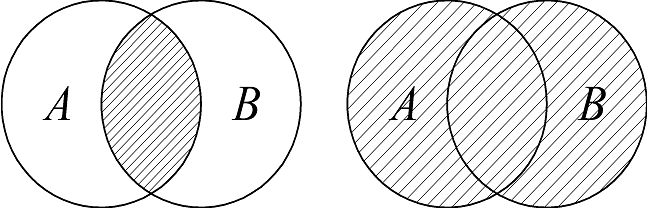
СУММА ПРОИЗВЕДЕНИЕ
Рис. 6. Диаграммы Венна суммы и произведения случайных событий.
При рассмотрении суммы исходных событий предполагается, что известны исходные вероятности Р(Аi) для n совместных событий Аi (i=1,2,….,n).
Теорема сложения вероятностей позволяет определить вероятность появления сложного события А.
Вероятность суммы нескольких несовместных событий равна сумме вероятностей этих событий.
Р(А) = Р(А1 + А2 +. . . .+ Аi +. . . .+Аn)
или
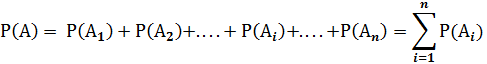
Если появление хотя бы одного из n несовместных событий является достоверным событием, то события Аi составляют полную группу несовместных событий, для которых выполняется нормирующее соотношение:
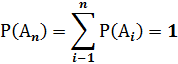
В том случае, когда события А и В совместны, сумма их вероятностей находится следующим образом: Р(С) = Р(А) + Р(В) – Р(АВ)
Сумма вероятностей трёх совместных событий:
P(D) = P(A) + P(B) + P(C) – P(AB) – P(BC) – P(AC) + P(ABC)
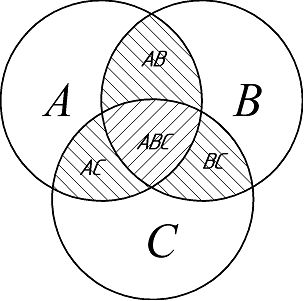
Рис. 7. Диаграмма Венна произведения трех совместных событий.
Перед рассмотрением теоремы умножения вероятностей введем несколько понятий:
— событие А называется независимым от события В если вероятность события А не зависит от того, произошло событие В или нет;
— событиеА называют зависимым от события В если вероятность события А изменяется в зависимости от того, произошло событие В или нет;
— вероятность события А, вычисленная при условии, что имело место другое событие В, называют условной вероятностью события А: Р(А|В).
Вероятность произведения n НЕЗАВИСИМЫХ СОВМЕСТНЫХ событий равна произведению вероятностей этих событий:
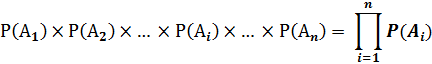
В частном случае, когда вероятности всех события равны, имеем:
Р(Аi) = Р; Р(А) = Рn
Вероятность произведения двух ЗАВИСИМЫХ СОВМЕСТНЫХ событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое имело место:
Р(АВ) = Р(А)×Р(В|А)
Вероятность произведения n ЗАВИСИМЫХ СОВМЕСТНЫХ событий равна произведению вероятности этих событий, причем вероятность каждого последующего по порядку события вычисляется при условии, что все предыдущие имели место:
P(A1×A2×. . . ×An-1×An) = P(A1)×P(A2|A1)×P(A3|A1A2)×…×P(An|A1……An-1)
2.1.4. Характеристики случайных величин.
Все разнообразие случайных величин (СВ) имеет одну общую характерную особенность, заключающуюся в том, что все СВ являются такими переменными величинами, которые в зависимости от исхода испытаний могут принимать то или иное (но только одно) возможное значение. Какое именно значение примет СВ определить до проведения испытания невозможно. Однако знание всех возможных значений СВ еще не позволяет полностью описать СВ. Важно также знать, как часто следует ожидать появление тех или иных возможных значений в результате повторения испытания в одних и тех же условиях. Для этого необходимо знать закон распределения СВ.
Законом распределения СВ называется всякое соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.
Формы, в которых может быть задан закон распределения дискретной СВ, могут быть различными. Простейшей формой задания распределения дискретной СВ является таблица следующего вида:
| Х | Х1 | Х2 | … | Хn |
| Р | Р1 | Р2 | … | Рn |
Такую таблицу называют рядом распределения СВ Х.
Иногда используют наглядное представление — графическое. По оси абсцисс откладывают значения СВ, а по оси ординат — вероятности соответствующие этим значениям. Полученная фигура называется многоугольником распределения.
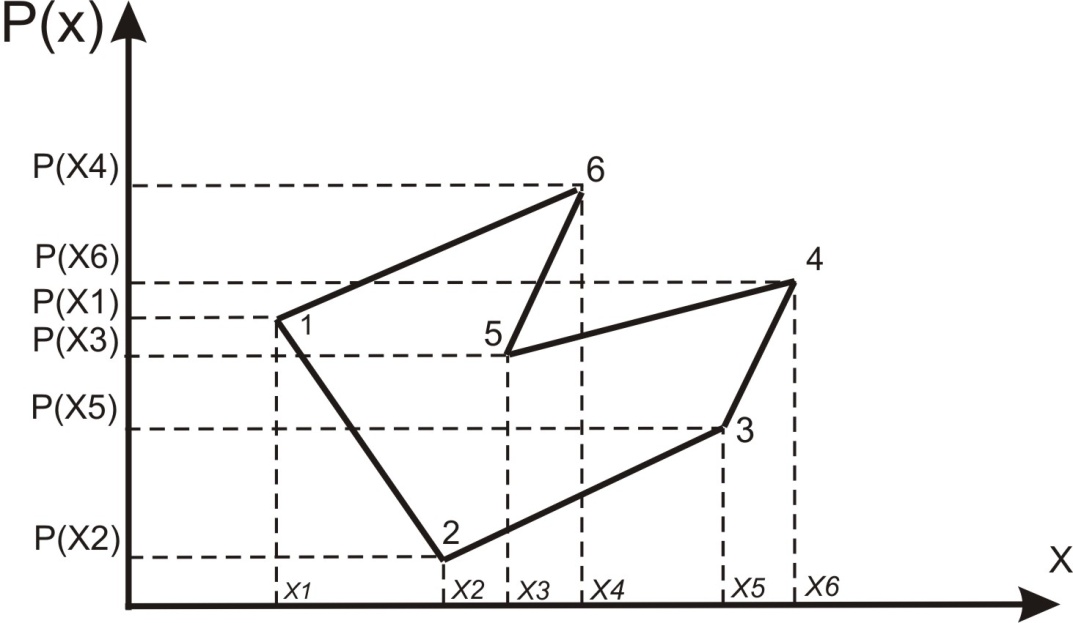
Рис. 8. Многоугольник распределения СВ Х.
Для количественной оценки характеристики распределения непрерывной СВ Х удобно воспользоваться не вероятностью события Х= х, а вероятностью события Х 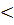 х, где «х» — текущая переменная.
х, где «х» — текущая переменная.
Функция распределения дискретной СВ разрывна и возрастает скачками при переходе возможных значений дискретной СВ. Совокупность вероятностей всего ряда значений данной дискретной СВ выражается в виде ступенчатой функции распределения вероятностей.
Если представить, что число n возможных значений дискретной СВ бесконечно возрастает, а промежутки между ними становятся все меньше и меньше, то в пределе можно получить гладкую или непрерывную кривую F(x).
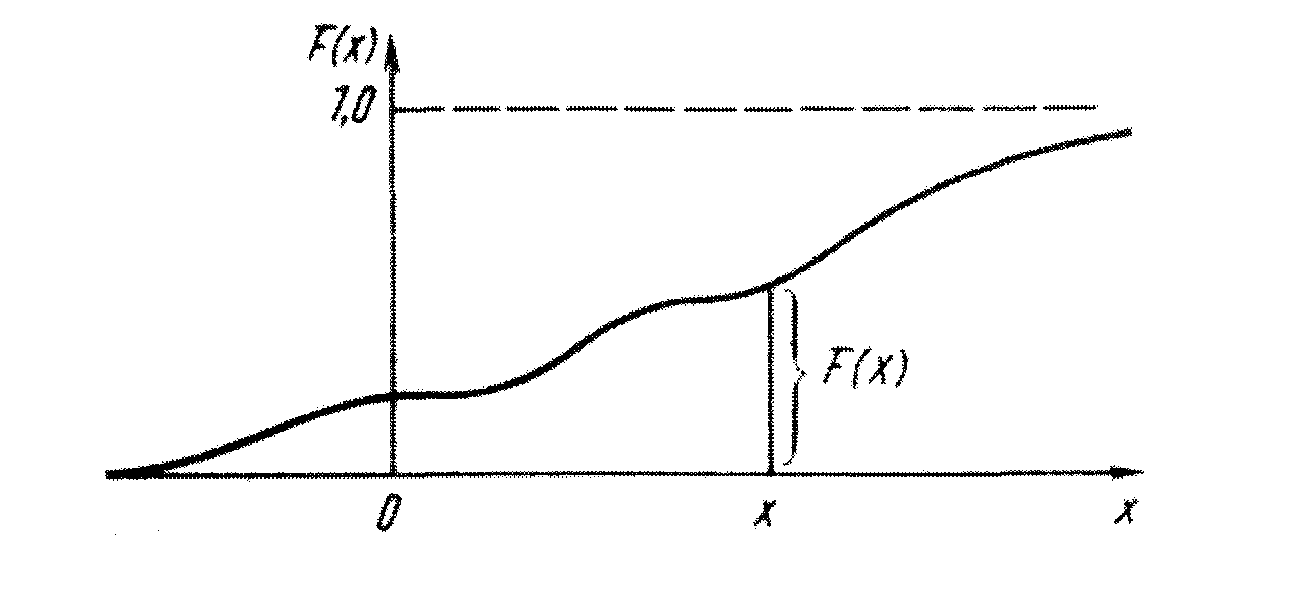
Рис. 9. Функция распределения СВ.
При решении практических задач часто оказывается необходимым вычислить вероятность того, что СВ примет значение, заключающееся в некоторых пределах. В этом случае вероятность появления СВ в интервале (α, β) (на рисунке 10), полузамкнутом слева (включая αи исключая β), равна разности значений функции распределения в концах интервала, т.е.:
Р(α ≤ х ≤ β) = F(β) - F(α)
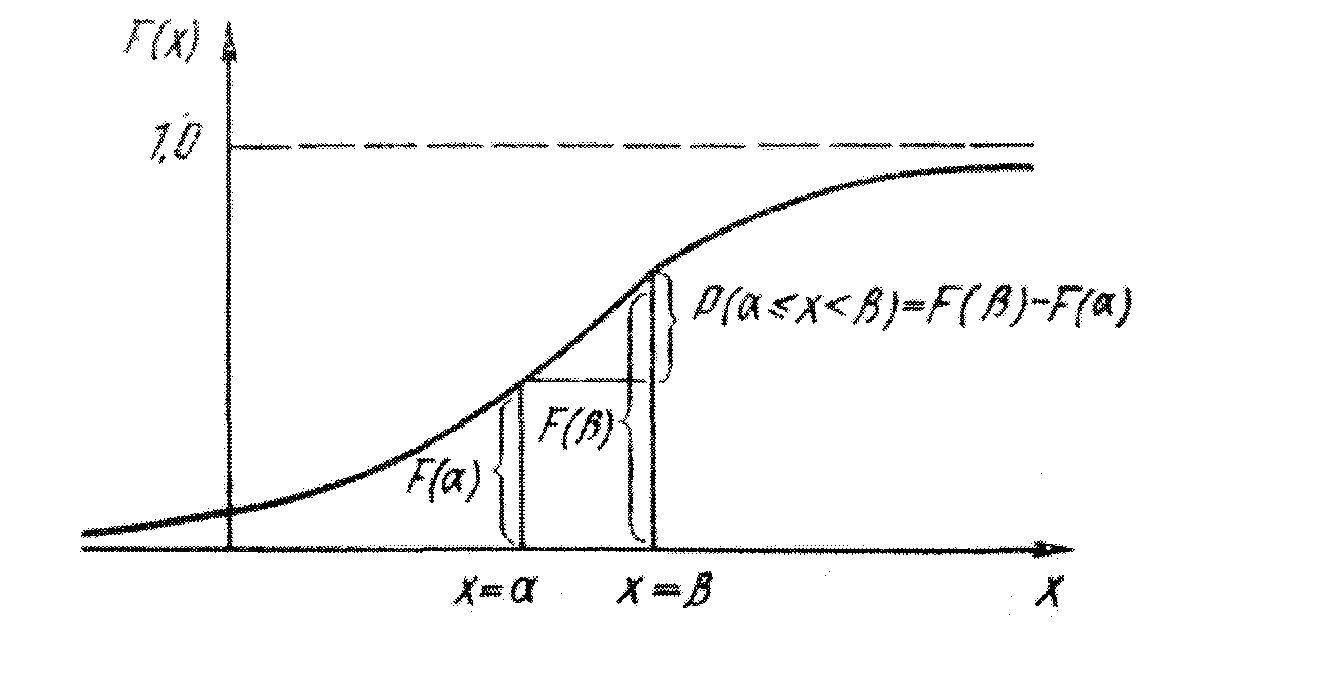
Рис. 10. К определению вероятности появления СВ в заданном интервале.
Функция распределения непрерывной СВ является её исчерпывающей вероятностной характеристикой. Но она имеет недостаток, заключающийся в том, что по ней трудно судить о характере распределения СВ в небольшой окрестности той или иной точки на числовой оси. Поэтому вводится особая функция, которая называется плотностью распределения вероятности или плотностью распределений.
Такая функция находится путем дифференцирования функции распределения непрерывной СВ F(x). (Для дискретной СВ функция плотности распределения не существует).
f(x) = dF(x)/dx
Таким образом, плотность распределения f(x) равна производной от функции распределения F(x) и её смысл состоит в том, что она указывает, как часто появляется СВ в малой окрестности х при повторении испытаний.
Вероятность попадания непрерывной СВ на участок (α, β)равна интегралу от плотности распределения, взятому по этому участку:
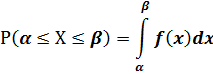
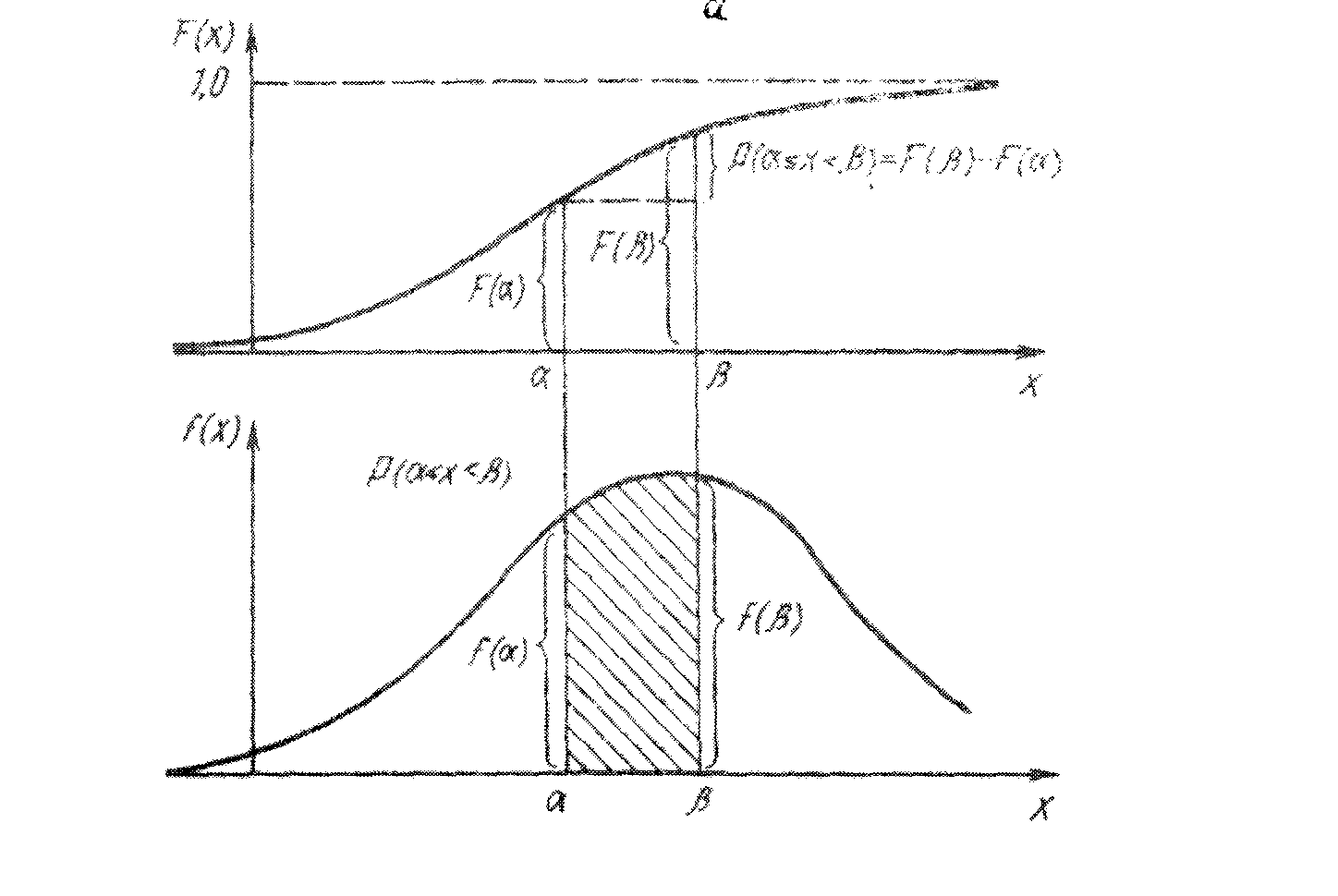
Рис. 11. Примеры графиков функций распределения СВ и плотности распределения СВ.
Дата добавления: 2016-09-26; просмотров: 3783;











