Параметры законов распределения случайных величин.
Получение вероятностных законов распределения, как правило, связано с целым рядом трудностей и сложностью эксперимента. Поэтому для вероятностного описания СВ используют некоторые числовые характеристики, являющиеся параметрами законов распределения СВ.
Математическим ожиданием или средним значением СВ называют постоянное число, около которого с ростом числа испытаний устойчиво колеблется среднее арифметическое значение СВ, найденное по опытным данным.
Для дискретной СВ (например числа отказов) математическое ожидание выражается:
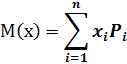
Для непрерывной СВ Х математическое ожидание находится по формуле:
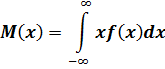
Другими словами, математическое ожидание СВ — это сумма произведений всех возможных значений СВ на вероятности этих значений.
Дисперсия СВ — математическое ожидание квадрата отклонения СВ от её математического ожидания.
Если математическое ожидание есть центр рассеивания СВ, то дисперсия характеризует рассеивание СВ около этого центра:
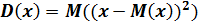
Для дискретной СВ дисперсия вычисляется как сумма:
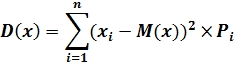
Для непрерывной СВ:
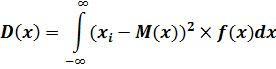
Среднее квадратичное отклонение СВ — квадратный корень от дисперсии СВ:
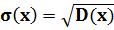
Дата добавления: 2016-09-26; просмотров: 2592;











