Частота или статистическая вероятность. Закон больших чисел.

В тех случаях, когда случайные события не сводятся к схеме случаев, для определения вероятности события можно использовать экспериментальный подход. С этой целью ставится серия из nопытов, в каждом из которых появляется или не появляется событие А. Отношение числа опытов в которых появилось событие Ак общему числу произведенных опытов называется частотой события А или его статистической вероятностью:

,

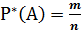где m – число опытов в которых появилось событие А; n – общее число опытов.

Увеличивая число опытов, можно добиться того, что частота события будет сколь угодно мало отличаться от его вероятности в отдельном опыте. Это утверждение следует из закона больших чисел.

(Общий принцип, в силу которого действие случайных факторов приводит при некоторых весьма общих условиях к результату, почти не зависящему от случая).

Если вероятность наступления некоторого события А последовательности n независимых испытаний постоянна и равна Р, то каким бы малым положительным числом не было бы ε с вероятностью сколь угодно близкой к 1, при достаточно большом n разность (m/n)-P по абсолютной величине окажется меньше ε.

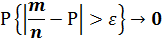
Случайные события количественно оцениваются случайными величинами.

Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, причем неизвестно заранее, какое именно.

К случайным величинам в качестве примера можно отнести:

— продолжительность срока службы t, t_ср, t_рем и т.д.;

— количество отказов m определенной группы однотипных изделий в течение заданного времени наработки;

— частоту появления отказов однотипных изделий m/N (где N – общее число изделий, участвующих в испытаниях).

Случайные величины могут быть:

— дискретными, т.е. СВ, принимающие отдельные друг от друга значения, которые можно пересчитать заранее (число отказов m, число посадок до появления первого отказа и т.д.);

— непрерывными, т.е. СВ, возможные значения которых непрерывно заполняют некоторый промежуток (например время наработки до отказа).