Кинематика вращательного движения
Понятие о вращательном движении
Различают четыре типа вращения: вращение вокруг неподвижной оси, вращение вокруг свободных осей, движение с одной неподвижной точкой (гироскоп), плоское движение (поступательное движение с полюсом  вращение вокруг этого полюса, например, шар или цилиндр, катящиеся по плоской поверхности).
вращение вокруг этого полюса, например, шар или цилиндр, катящиеся по плоской поверхности).
Будем рассматривать только вращение тела вокруг неподвижной оси (см. рис. 23).
Вращательное движение вокруг неподвижной оси – это движение твёрдого тела, при котором какие-либо две его точки (т. 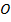 и т.
и т. 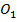 ) остаются всё время неподвижными.
) остаются всё время неподвижными.
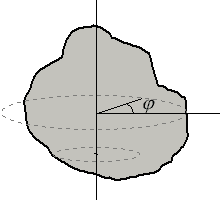 Рис. 24.
Рис. 24.
|
Прямая
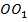 , проходящая через эти точки, называется осью вращения. Все точки тела при таком вращении описывают окружности в плоскостях, перпендикулярных оси вращения, и с центрами, лежащими на этой оси (рис. 24); имеют различные линейные скорости
, проходящая через эти точки, называется осью вращения. Все точки тела при таком вращении описывают окружности в плоскостях, перпендикулярных оси вращения, и с центрами, лежащими на этой оси (рис. 24); имеют различные линейные скорости 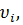 но при этом поворачиваются на равные углы
но при этом поворачиваются на равные углы 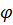 .
.
Угловая скорость
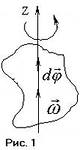 Рис. 25.
Рис. 25.
|
Быстроту и направление вращения твёрдого тела характеризует угловая скорость вращения
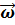 (рис. 25).
(рис. 25).
Угловой скоростью называют вектор  который численно равен первой производной от угла поворота
который численно равен первой производной от угла поворота 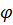 по времени и направлен вдоль неподвижной оси вращения так, чтобы из его конца вращение тела было видно происходящим против часовой стрелки (рис. 24):
по времени и направлен вдоль неподвижной оси вращения так, чтобы из его конца вращение тела было видно происходящим против часовой стрелки (рис. 24):
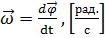 ,
,
где 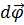 –вектор элементарного поворота.
–вектор элементарного поворота.
Вращение тела называется равномерным, если численное значение его угловой скорости не изменяется с течением времени: 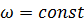 .
.
Для равномерного вращения справедливо соотношение: 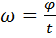 .
.
Равномерное вращение характеризуется периодом и частотой вращения.
Периодом вращения 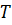 называется промежуток времени, за который равномерно вращающееся тело, совершает один полный оборот (т.е. поворачивается на угол
называется промежуток времени, за который равномерно вращающееся тело, совершает один полный оборот (т.е. поворачивается на угол 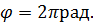 ):
):
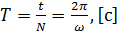 ,
,
где 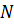 – число полных оборотов, совершаемых телом за время
– число полных оборотов, совершаемых телом за время 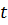 .
.
Частота вращения 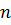 – число оборотов, совершаемых телом за единицу времени:
– число оборотов, совершаемых телом за единицу времени:
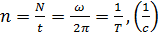 ,
,
т.е. 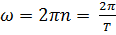 .
.
Неравномерное вращение– вращение с переменной угловой скоростью, т.е. 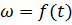 .
.
Угловое ускорение
Неравномерное вращение характеризуется угловым ускорением 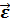 ,которое показывает быстроту изменения угловой скорости.
,которое показывает быстроту изменения угловой скорости.
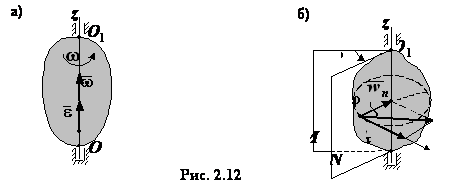 Рис. 26.
Рис. 26.
|
Угловым ускорением называется вектор
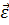 ,равный первой производной по времени от угловой скорости(рис. 26):
,равный первой производной по времени от угловой скорости(рис. 26):
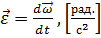 или
или 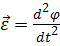 .
.
Модуль углового ускорения – величина алгебраическая:
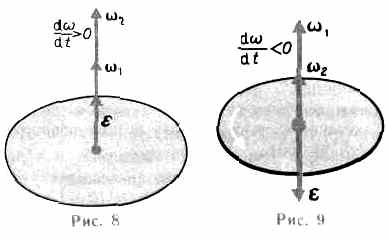
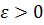 –ускоренное вращение;
–ускоренное вращение; 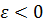 –замедленное вращение (рис. 27).
–замедленное вращение (рис. 27).
Т.е. вектор углового ускорения 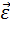 направлен вдольоси вращения (в сторону
направлен вдольоси вращения (в сторону 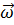 при укоренном вращении и противоположно
при укоренном вращении и противоположно 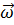 –при замедленном вращении).
–при замедленном вращении).
Вращение с постоянным ускорением 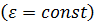 называетсяравнопеременным вращением (равноускоренным или равнозамедленным).
называетсяравнопеременным вращением (равноускоренным или равнозамедленным).
Для равнопеременного вращения справедливы соотношения:
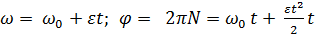 ,
,
где 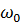 –начальная угловая скорость;
–начальная угловая скорость; 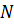 –число полных оборотов тела.
–число полных оборотов тела.
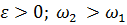 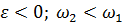 ускоренное вращение; замедленное вращение;
ускоренное вращение; замедленное вращение;
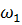 –начальная угловая скорость.
Рис. 27. –начальная угловая скорость.
Рис. 27.
|
Аналогия между кинематикой поступательного и вращательного движений
| Поступательное движение | Вращательное движение |
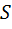 –путь –путь
| 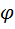 – угол поворота – угол поворота
|
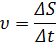
| 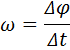
|
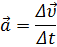
| 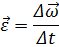
|
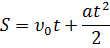
| 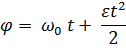
|
Связь между кинематическими величинами, характеризующими поступательное и вращательное движения
Между кинематическими величинами, характеризующими поступательное и вращательное движения тела, существует простая связь:
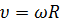 ;
;
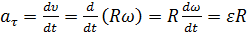 ;
;
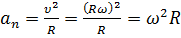 .
.
Динамика
Предмет динамики
Динамика – раздел механики, посвящённый изучению движения материальных тел с учётом причин их вызывающих.
Масса. Инерция
Под инерцией (от лат.Inertia–бездеятельность, косность) понимают свойство тела сохранять состояние своего движения или покоя (в инерциальной системе отсчёта), когда внешние воздействия на тело отсутствуют или взаимно уравновешиваются, и изменять эти состояния тем медленнее, когда внешние воздействия не уравновешиваются.
Инертность у различных тел проявляется в разной степени. Мерой инертности тел является масса.
Масса 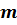 –cкалярная физическая величина, являющаяся мерой инерции (во втором законе Ньютона:
–cкалярная физическая величина, являющаяся мерой инерции (во втором законе Ньютона: 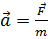 , гравитации (в законе всемирного тяготения:
, гравитации (в законе всемирного тяготения: 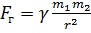 ) и энергии (в законе взаимосвязи массы и энергии:
) и энергии (в законе взаимосвязи массы и энергии: 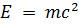 ).
).
В СИ: 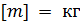 [6] .
[6] .
В релятивистском случае ( 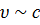 ) справедливо следующее:
) справедливо следующее:
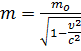 ,
,
где 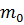 – масса покоя
– масса покоя 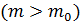 .
.
Плотность тела – масса единицы объёма тела: 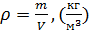 .
.
Сила
Сила 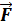 - это векторная величина, являющаяся мерой механического воздействия на рассматриваемое тело со стороны других тел или полей.
- это векторная величина, являющаяся мерой механического воздействия на рассматриваемое тело со стороны других тел или полей.
В СИ: 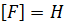 [7] (ньютон).
[7] (ньютон).
В результате действия силы тело изменяет свою скорость, либо деформируется.
Силы бывают внешние и внутренние.
Внешние силы – силы, действующие на систему стороны внешних тел.
Внутренние силы – это силы взаимодействия между частями рассматриваемой системы.
Механическая система тел называется замкнутой (изолированной), если она не взаимодействует с внешними телами, т.е. на неё внешние силы не действуют 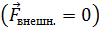 .
.
Понятие изолированной системы – это идеализация, т.е. таких систем реально не существует.
Различают так же силы консервативные и неконсервативные.
Консервативной (потенциальной) силой называется сила, работа которой зависит только от начального и конечного положения точки её приложения и не зависит от вида её траектории (например, консервативные силы: сила тяжести, сила упругости, кулоновская (электростатическая) сила).
Остальные силы – неконсервативные.
Неконсервативные силы подразделяются на диссипативные[8] и гироскопические.
Диссипативные силы – силы, полная работа которых отрицательная (например: сила трения, сила сопротивления).
Гироскопические силы – силы, зависящие от скорости тела и действующие перпендикулярно этой скорости (например: центростремительные силы; сила Лоренца, действующая со стороны магнитного поля, на движущийся в этом поле электрический заряд).
Гироскопические силы энергию тела не изменяют и работы не совершают.
Сложение сил–нахождение геометрической суммы (т.н. главного вектора) данной системы сил путем последовательного применения правила параллелограмма сил или построения силового многоугольника. Для сил, приложенных в одной точке, при сложении сил определяется их равнодействующая 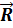 (рис. 28).
(рис. 28).
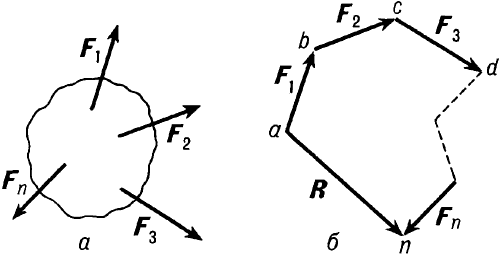 Рис. 28.
Рис. 28.
|
Пример.
Если к телу приложены две силы в одной точке, то равнодействующая этих сил равна: 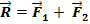 (рис. 29).
(рис. 29).
Модуль равнодействующей двух сил можно определить по теореме косинусов:
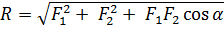 ,
,
или при 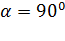 – по теореме Пифагора.
– по теореме Пифагора.
U AAYACAAAACEA1Pz1ut8AAAAKAQAADwAAAGRycy9kb3ducmV2LnhtbEyPS0/DMBCE70j8B2uRuLVO Qx8Q4lQVFRcOSBSkcnTjTRzhl2w3Df+e5QSn1WhGs9/U28kaNmJMg3cCFvMCGLrWq8H1Aj7en2f3 wFKWTknjHQr4xgTb5vqqlpXyF/eG4yH3jEpcqqQAnXOoOE+tRivT3Ad05HU+WplJxp6rKC9Ubg0v i2LNrRwcfdAy4JPG9utwtgKOVg9qH18/O2XG/Uu3W4UpBiFub6bdI7CMU/4Lwy8+oUNDTCd/diox I6B8WNKWLGBW0qXAenG3AXYip1iugDc1/z+h+QEAAP//AwBQSwECLQAUAAYACAAAACEAtoM4kv4A AADhAQAAEwAAAAAAAAAAAAAAAAAAAAAAW0NvbnRlbnRfVHlwZXNdLnhtbFBLAQItABQABgAIAAAA IQA4/SH/1gAAAJQBAAALAAAAAAAAAAAAAAAAAC8BAABfcmVscy8ucmVsc1BLAQItABQABgAIAAAA IQABsgRMhwIAABwFAAAOAAAAAAAAAAAAAAAAAC4CAABkcnMvZTJvRG9jLnhtbFBLAQItABQABgAI AAAAIQDU/PW63wAAAAoBAAAPAAAAAAAAAAAAAAAAAOEEAABkcnMvZG93bnJldi54bWxQSwUGAAAA AAQABADzAAAA7QUAAAAA " stroked="f">
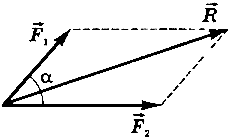 Рис. 29.
Рис. 29.
|
Примеры сил в механике
1).Сила гравитации (закон всемирного тяготения)
Исторический очерк
 Рис. 30.
Рис. 30.
Сама идея всеобщей силы тяготения неоднократно высказывалась и до Ньютона. Ранее о ней размышляли Эпикур, Гассенди, Кеплер, Борелли, Декарт, Роберваль, Гюйгенс и другие.
Исаак Ньютон.
[9]. Без преувеличения один из величайших научных умов за всю историю человечества. Именно Ньютону мы обязаны той картиной физического мира, которая сложилась к сегодняшнему дню.
Кеплер полагал, что тяготение обратно пропорционально расстоянию до Солнца и распространяется только в плоскости эклиптики; Декарт считал его результатом вихрей в эфире. Но до Ньютона никто не сумел ясно и математически доказательно связать закон тяготения (силу, обратно пропорциональную квадрату расстояния) и законы движения планет (законы Кеплера).В своём основном труде «Математические начала натуральной философии» (1687) Исаак Ньютон вывел закон тяготения, основываясь на эмпирических законах Кеплера, известных к тому времени. Теория Ньютона, в отличие от гипотез предшественников, имела ряд существенных отличий. Ньютон опубликовал не просто предполагаемую формулу закона всемирного тяготения, но фактически предложил целостную математическую модель.
Дата добавления: 2016-09-26; просмотров: 2266;











