Замкнутая векторная СМО с отказами в обслуживании

Как и в главе 3, рассматривая замкнутую векторную СМО с неоднородным входящим потоком, будем предполагать, что заявка требует для своего обслуживания несколько приборов, которые занимаются этой заявкой и освобождаются одновременно, и длительность ее обслуживания имеет экспоненциальное распределение. Будем также предполагать, что тип заявки определяется не только числом требуемых для ее обслуживания приборов, но и номером отправившего ее источника, т.е. (s,i) – заявка, поступившая от s-го источника и требующая q_i приборов для своего обслуживания, интенсивность обслуживания которой – 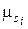, , 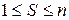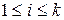(n – число источников в системе, k – максимальное число обслуживающих приборов, требуемых заявкой).

Состояние замкнутой СМО определяется [11, 12] матрицей R:

,

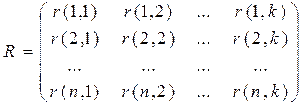где при 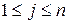r(j, i) = 1, если i-заявка от j-го источника находится на обслуживании, и r(j,i) = 0 в противном случае. Отметим, что в каждой строке матрицы R может быть не более одной единицы, но эта единица может находиться на любом месте в строке, где .

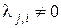Для замкнутой СМО суммарная интенсивность i- заявок

.

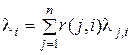Кроме ограничения, что в каждой строке матрицы R может быть не более одной единицы, имеется еще одно ограничение, накладываемое конечностью числа N обслуживающих приборов в системе: для R должно выполняться неравенство

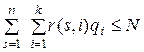, (5.11)

так как число приборов, занятых обслуживанием всех находящихся в СМО заявок, не может быть больше числа всех имеющихся в системе приборов.

Если при выполнении условий (5.11) выполняется неравенство, то в замкнутой СМО складывается ситуация, аналогичная ситуации потери заявок для открытых систем, так как при этом имеются неблокированные источники, генерирующие заявки, для обслуживания которых может оказаться недостаточно свободных приборов. В состоянии R число свободных приборов

.

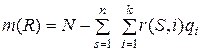Для исследования таких ситуаций и их вероятностей необходимо знать распределение вероятностей P(R) состояний R замкнутой СМО.

Выделим четыре состояния: R(0,0), R(1,0), R(0,1), R(1,1) – рассматриваемой системы. Состояния R(v₁, v₂) характеризуются тем, что в матрице R выделены два элемента: r(s₁, i₁) и r(s₂, i₂), которые принимают значения r(s₁, i₁) = v₁, r(s₂, i₂) = v₂. Значения остальных элементов r(s, i) матрицы R(v₁, v₂) совпадают. Все четыре состояния R(v₁, v₂) удовлетворяют неравенству (5.11). Рассматривая интенсивности переходов между выделенными состояниями случайного марковского процесса изменения состояний системы обслуживания, получим

, ,

, ,

, ,

, .

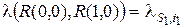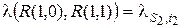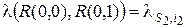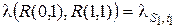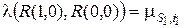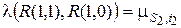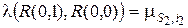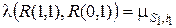Следовательно, выполняется равенство

.

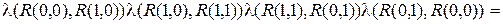
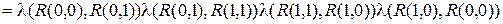Это равенство выполняется для любого цикла в графе переходов исследуемого марковского процесса, тогда в соответствии с критерием эквивалентности уравнений глобального и детального балансов [26] можно для вероятностей P(R) записать следующие равенства

,

.

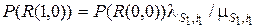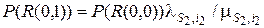Аналогичные равенства выполняются и для всех других состояний R, удовлетворяющих неравенству (5.11). Обозначим как P(0) вероятность состояния R = 0; здесь все элементы r(s, i) матрицы R равны нулю; 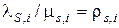. Тогда для любого состояния, удовлетворяющего неравенству (5.11), можно записать, что стационарное распределение вероятностей P(R) определяется равенством

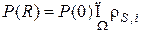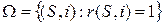, , (512а)

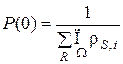. (5.12б)

Как обычно, вероятность P(0) определяется условием нормировки. Здесь суммирование происходит по всем R, элементы которых удовлетворяют (5.11). Если среди r_s,i имеются одинаковые, то в (5.12) появляются степени соответствующих значений r.

Равенство (5.12а) определяет мультипликативность распределения состояний рассматриваемой замкнутой СМО, а формула (5.12б) определяет это распределение в явном виде.

Знание явного выражения (5.12б) для распределения вероятностей P(R) состояний R замкнутой СМО позволяет определять ее различные вероятностные характеристики, например, такие, как вероятность блокировки источников с i-заявками, т.е. блокировки i-заявок; вероятность блокировки (s, i)-заявок; вероятность П блокировки произвольной заявки, которая не допускается к обслуживанию в связи с отсутствием достаточного для нee числа обслуживающих приборов.

Вероятностью П назовем отношение среднего числа 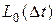заявок, мгновенно возвращенных в источник в связи с отсутствием достаточного для них числа свободных обслуживающих приборов, к среднему числу 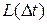всех заявок, обратившихся в систему обслуживания за время 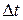, которые либо были приняты к обслуживанию, либо которым было отказано в обслуживании. Так как рассматриваем среднее стационарное распределение, то величина числа П не зависит от значений 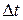, поэтому устремив 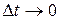, получим

,

,

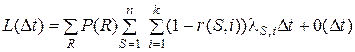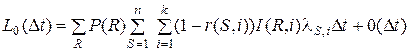где

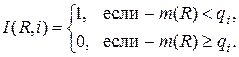
Таким образом,

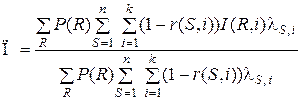. (5.13)

Пример 5.3 (замкнутой СМО). Пусть в СМО N обслуживающих приборов и три неоднородных источника, два из которых совпадают между собой, а третий отличается от них. Заявка каждого источника требует от 1 до 5 обслуживающих приборов. Так как два источника одинаковы, то в матрице l, определяющей структуру входного потока, две строки будут совпадать и матрица будет иметь размерность 3´5. Значения вероятностей П по (5.13) приведены в табл. 5.2 для трех различных матричных потоков, определяемых матрицей l, и различного числа N обслуживающих приборов ( 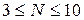). Итак, матрица l имеет следующий вид:

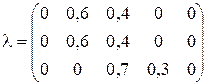. (5.14)

При этом два первых источника с интенсивностью 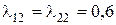генерируют потоки заявок, требующих для своего обслуживания два прибора, а с интенсивностью 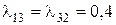– три прибора; третий источник с интенсивностью 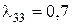требует три прибора для каждой своей заявки, а с интенсивностью 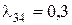– четыре прибора. Интенсивность заявок, требующих другое число приборов, равна нулю, т.е. = .

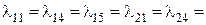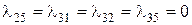При этом для матрицы (5.14) П = 0,188 для N = 3, П = 0,027 для N = = 5, П = 0,006 для N = 6. Заметим, что при N = 3 все заявки, требующие четыре прибора для своего обслуживания и поступающие с интенсивностью 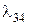= 0,3, вообще не обслуживаются.

Таблица 5.2

N	0,6 0,4 0 0 0 0,6 0,4 0 0 0 0,0 0,7 0,3 0 0	0 0,6 0,4 0 0 0 0,6 0,4 0 0 0 0,0 0,7 0,3 0	0 0 0,6 0,4 0 0 0 0,6 0,4 0 0 0 0,0 0,7 0,3
	1,82141´10–2	1,87769´10–1	7,07887´10–1
	4,24625´10–3	4,62260´10–2	2,01878´10–1
	1,11933´10–4	2,71095´10–2	6,75991´10–2
	2,32387´10–5	6,27853´10–3	6,27057´10–2
		5,29892´10–4	3,57826´10–2
		2,52949´10–4	8,37207´10–3
		4,78549´10–5	1,21902´10–3
			9,72612´10–4