Используя нормировочное условие

,

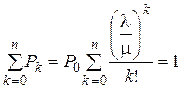получаем

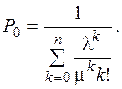
Окончательно получим следующие формулы для вероятностей состояний:

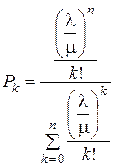(k = 0,1,2, ... ,n), (3.13)

которые называются формулами Эрланга.

Введем обозначение ρ = λ/μ. Преобразуем выражение (3.13) к виду, удобному для вычислений. С этой целью используем ρ и умножим числитель и знаменатель дроби (3.13) на величину .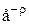

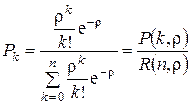, (3.14)

где P(k, ρ) и R(n, ρ) – табличные функции пуассоновского распределения.

Найдем характеристики классической системы массового обслуживания с отказами.

С одной стороны, вероятность обслуживания заявки Р_обс, очевидно, равна вероятности того, что заявка, поступившая в систему, застанет свободным хотя бы один канал:

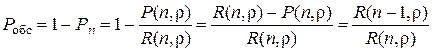. (3.15)

С другой стороны, вероятность обслуживания заявки равна относительной пропускной способности системы:

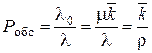, (3.16)

где λ₀ – плотность потока обслуженных заявок (абсолютная пропускная способность СМО), а 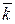– среднее число занятых каналов. Отсюда

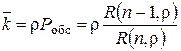. (3.17)

Выражение для среднего числа занятых каналов 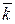можно получить и непосредственно через вероятность Р_k:

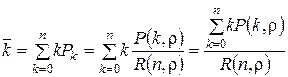. (3.18)

Сравнивая (3.17) и (3.18), убеждаемся в том, что

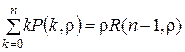. (3.19)

Вероятность того, что канал занят, будет равна отношению среднего числа занятых каналов 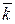к общему числу каналов n:

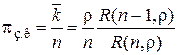. (3.20)

Введем в рассмотрение случайную величину Т_з.к – время занятости канала, равное длине промежутка времени, начинающегося с момента поступления заявки в канал, до следующего непосредственного момента освобождения канала. Время занятости канала Т_з.к по условию распределено по показательному закону с интенсивностью μ. Следовательно, среднее время занятости канала

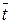_з.к = М[Т_з.к] = 1/μ.

Временем простоя канала Т_п.к называется длина промежутка времени, начинaющегося с момента освобождения канала, до его занятия следующей заявкой. Среднее время простоя канала 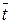_п.к определяется из следующего выражения, имеющего место для эргодической системы, находящейся в стационарном режиме:

,

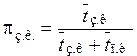т.е. вероятность занятости канала равна отношению среднего времени занятости канала к сумме среднего времени занятости канала и среднего времени простоя канала. Отсюда

.

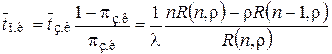Вероятность полной загрузки системы, т.е. вероятность того, что все каналы будут заняты:

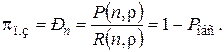
Аналогичным образом могут быть определены и другие характеристики системы.