Системы массового обслуживания с отказами
Классическая система массового обслуживания с отказами (система Эрланга)
Постановка задачи. На вход n-канальной СМО подается простейший поток заявок с интенсивностью λ. Интенсивность простейшего потока обслуживания каждого канала обозначим μ. Если заявка застала все n каналов занятыми, то она получает отказ (покидает систему не обслуженной). Если заявка застала свободным хотя бы один канал, то она принимается к обслуживанию любым из свободных каналов и обслуживается до конца (заявки «терпеливые»).
Описанная выше система названа нами классической потому, что с рассмотрения такой системы Эрлангом и начала развиваться теория массового обслуживания. Эрланг рассматривал работу такой системы на примере работы автоматического телефонного узла связи. В этом случае поток заявок представляет собой поток вызовов со стороны абонентов. Длительность обслуживания характеризуется длительностью коммутации и длительностью разговора. Число каналов n равняется максимально возможному числу одновременно осуществляемых разговоров.
Анализ работы СМО начнем с рассмотрения возможных состояний системы и составления размеченного графа состояний с указанием интенсивностей потоков, переводящих систему из одного состояния в другое.
Рассмотрим следующее множество состояний системы:
x0 – все каналы свободны, ни одна заявка не обслуживается;
x1 – занят ровно один канал (какой – не важно), обслуживается одна заявка;
xk – занято ровно k каналов (каких именно – не важно), обслуживается k заявок;
xn – все n каналов заняты, обслуживается n заявок.
Граф состояния данной СМО с отказами в обслуживании представлен на рис. 3.6.

Рис. 3.6. Граф состояний СМО с отказами в обслуживании
Как и в § 3.3, возможность перескока «через состояние» не рассматривается, т.к. все потоки ординарные. Поясним порядок определения интенсивностей потоков событий на рис. 3.6. Когда система находится в состоянии x0, на нее действует поток заявок с интенсивностью λ, переводящий систему в состояние x1. Если система находится в состоянии x1, то на нее действует уже два потока событий: а) поток заявок с интенсивностью λ, который стремится перевести систему в состояние x2; б) поток освобождений канала («поток обслуживаний»), который стремится перевести систему в состояние x0. Интенсивность этого потока равна μ.
Рассмотрим случай, когда система находится в состоянии xk (k = 1, 2, ... , n–1). В этом состоянии на систему действует также два потока: а) поток заявок с интенсивностью λ, который стремится перевести систему в состояние xk+1; б) поток освобождений всех занятых каналов с интенсивностью kμ, который стремится перевести систему справа налево в состояние xk–1.
Если система находится в состоянии xn, то на нее действует только один поток событий с интенсивностью nμ, переводящий систему справа налево в состояние xn–1.
Система уравнений имеет следующий вид:

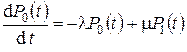 ,
,
............................................
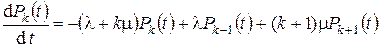 , k = 1,2,…, n–1, (3.10)
, k = 1,2,…, n–1, (3.10)
............................................
 .
.
Система (3.10) интегрируется при следующих начальных условиях:
Р0(0) = 1; Рk(0) = 0 (k = 1,2, ... , n),
что соответствует случаю, когда система в начальный момент времени t = 0 свободна. Решение системы (3.10) при данных начальных условиях удовлетворяет нормировочному условию
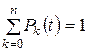 (t ≥ 0). (3.11)
(t ≥ 0). (3.11)
Уравнения (3.10) называются уравнениями Эрланга. Заметим, что (3.10) и (3.11) справедливы и для случая, когда потоки событий не являются простейшими, а представляют собой нестационарные пуассоновские потоки. В этом случае параметры λ = λ(t) и μ = μ(t).
Рассмотрим стационарный режим работы при t → ∞. Такой режим существует (см. § 3.3), т.к. рассматриваемая система эргодична. Поэтому при t → ∞ система (3.10) превращается в систему алгебраических уравнений:
 0 = –λ Р0 + μР1,
0 = –λ Р0 + μР1,
.……………..
0 = –(λ + kμ)Рk + λРk–1+ (k + 1)μ Рk +1 (k = 1,2, ... , n–1),
.…………….
0 = + λРn–1 – nμ Рn = 0,
которую нужно решать совместно с (3.11).
Введем обозначение:
ui = –λPi–1 + iμ Рi (k = 1,2, ... , n),
тогда
 u1 = 0,
u1 = 0,
……...
uk+1 – uk = 0 (k = 1,2, ... , n–1), (3.12)
……...
un = 0.
Анализируя (3.12), убеждаемся в том, что ui = 0. Следовательно,
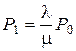 ;
; 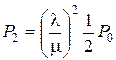 ;
; 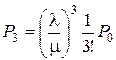 ;
; 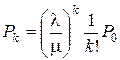 .
.
Дата добавления: 2021-01-11; просмотров: 646;











