Гипотеза плоских сечений (гипотеза Бернулли).

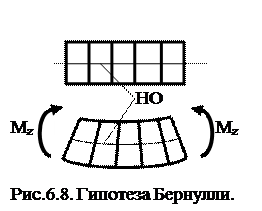Сечения плоские до и после деформации, они только поворачиваются относительно некоторой линии, которая называется нейтральной осью балки (НО). При этом волокна балки, лежащие с одной стороны от нейтральной оси будут растягиваться, а с другой – сжиматься; волокна, лежащие на нейтральной оси своей длины не изменяют;

2) Гипотеза о постоянстве нормальных напряжений. Напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса;

3) Гипотеза об отсутствии боковых давлений. Соседние продольные волокна не давят друг на друга.

Связь между внутренними усилиями и нормальными напряжениями в сечении балки найдем из рассмотрения напряжений в элементарной площадке dF, выделенной в поперечном сечении F балки в точке с координатами у и z (ось y для удобства анализа направлена вниз):

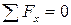, следовательно 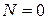, поэтому

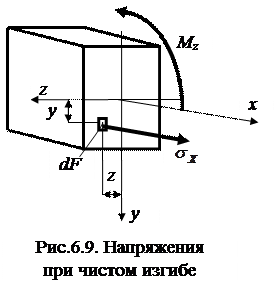
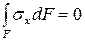; (6.10)

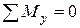, следовательно 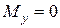, поэтому

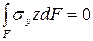; (6.11)

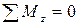, следовательно 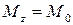, поэтому

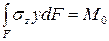; (6.12)

Как видим, неизвестен характер распределения нормальных напряжений по сечению. Для решения задачи рассмотрим геометрическую картину деформаций.

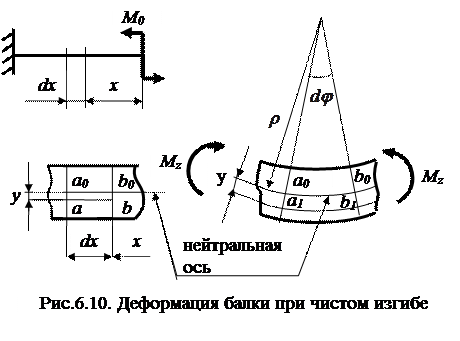Рассмотрим деформацию элемента балки длиной dx, выделенного из изгибаемого стержня в произвольной точке с координатой x. Учитывая принятую ранее гипотезу плоских сечений, после изгиба сечения балки повернутся относительно нейтральной оси (НО) на угол 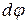, при этом волокно ab, отстоящее от оси на расстояние у, превратится в дугу окружности a₁b₁, а его длина изменится на некоторую величину.

Здесь напомним, что длина волокон, лежащих на нейтральной оси, не изменяется а потому дуга a₀b₀ (радиус кривизны которой обозначим 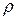), имеет ту же длину, что и отрезок a₀b₀ до деформации: a₀b₀=dx.

Найдем относительную линейную деформацию 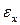, волокна ab изогнутой балки: 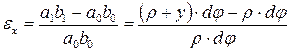, следовательно

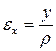(6.13)

Учитывая, что, в соответствии с гипотезой об отсутствии боковых давлений, запишем закон Гука для изгиба в виде:

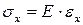(6.14)

Из формулы для относительной линейной деформации с учетом закона Гука получим закон распределения нормальных напряжений по сечению балки:

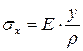. (6.15)

Подставляя это выражение в каждое из уравнений равновесия, имеем следующие соотношения:

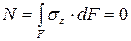, следовательно 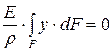, отсюда

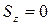; (6.16)

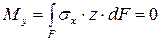, следовательно 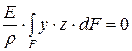, отсюда

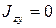; (6.17)

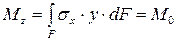, следовательно 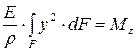, отсюда

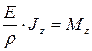. (6.18)

Из анализа (6.16) и (6.17) следует, что оси у и z являются главными осями сечения, а нейтральная ось проходит через центр тяжести сечения.

Из (6.18) получим формулу для определения кривизны бруса при изгибе

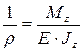, (6.19)

Используя это выражение, получим формулу определения нормальных напряжений при изгибе:

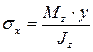.(6.20)

Из анализа полученного уравнения следует, что нормальные напряжения при изгибе равны нулю в точках, лежащих на нейтральной оси, и достигают экстремальных значений на поверхности балки, при .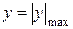

Максимальные нормальные напряжения при изгибе найдем по формуле:

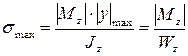,(6.21)

где W_z – осевой момент сопротивления

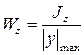. (6.22)

Таким образом, в случае изгиба условие прочности по нормальным напряжениямможет быть записано в следующем виде (для материала балки, одинаково сопротивляющегося растяжению-сжатию):

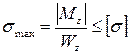.(6.23)