Внутренние силы. Метод сечений

Модели прочностной надежности

Задачи и методы сопротивления материалов

Сопротивление материалов – наука об инженерных методах расчета на прочность, жесткость и устойчивость конструкций, сооружений, машин и механизмов.

Прочность – способность конструкции, ее частей и деталей выдерживать определенную нагрузку не разрушаясь.

Жесткость - способность конструкции и ее элементов сопротивляться деформации (изменению формы и размеров).

Устойчивость - способность конструкции и ее элементов сохранять определенную начальную форму упругого равновесия.

Для того чтобы конструкции в целом отвечали требованиям прочности, жесткости и устойчивости, необходимо придать их элементам наиболее рациональную форму и определить соответствующие размеры. Сопротивление материалов решает указанные задачи, основываясь на теоретических и опытных данных.

В сопротивлении материалов широко применяются методы теоретической механики и математического анализа, используются данные из разделов физики, изучающих свойства различных материалов, материаловедения и других наук. К тому же сопротивление материалов является наукой экспериментально-теоретической, так как она широко использует опытные данные и теоретические исследования.

Модели прочностной надежности

Оценка прочностной надежности элемента конструкции начинается с выбора расчетной модели (схемы). Моделью называют совокупность представлений, условий и зависимостей, описывающих объект, явление.

Модели материала.

В расчетах прочностной надежности материал детали представляют однородной сплошной средой, что позволяет рассматривать тело как непрерывную среду и применять методы математического анализа.

Под однородностью материал понимают независимость его свойств от размеров выделенного объема.

Расчетная модель материала наделяется такими физическими свойствами, как упругость, пластичность и ползучесть.

Упругость – свойство тела (детали) восстанавливать свою форму после снятия внешней нагрузки.

Пластичность – свойство тела сохранять после разгрузки полностью или частично деформацию, полученную при нагружении.

Ползучесть – свойство тела увеличивать со временем деформацию при действии внешних сил.

Модели формы.

Конструкции имеют в большинстве случаев сложную форму, отдельные элементы которой можно свести к основным типам:

1. Стержнем или брусом называют тело, у которого два размера малы по сравнению с третьим.

Стержни могут быть с прямолинейными и криволинейными осями, а также постоянного или переменного сечения.

К прямым стержням относятся балки, оси, валы; к кривым – грузоподъемные крюки, звенья цепей и т.п.

2. Оболочка – тело, ограниченное двумя криволинейными поверхностями, расстояние между которыми мало по сравнению с прочими размерами.

Оболочки бывают цилиндрические, конические, сферические. К оболочкам относятся тонкостенные резервуары, котлы, купола зданий, корпуса судов, обшивки фюзеляжей, крыльев и т.п.

3. Пластина - тело, ограниченное двумя плоскими или слабоизогнутыми поверхностями, имеющее малую толщину.

Пластинами являются плоские днища и крышки резервуаров, перекрытия инженерных сооружений и т.п.

4. Массив или массивное тело – тело, у которого все три размера одного порядка.

Относятся: фундаменты сооружений, подпорные стенки и т.п.

Модели нагружения.

Силы являются мерой механического взаимодействия элементов конструкций. Силы бывают внешние и внутренние.

Внешние силы – это силы взаимодействия между рассматриваемым элементом конструкции и связанными с ним телами.

Внешние силы бывают объемными и поверхностными.

Объемные силы – это силы инерции и силы тяжести. Они действуют на каждый бесконечно малый элемент объема.

Поверхностные силы обнаруживаются при контактном взаимодействии данного тела с другими телами.

Поверхностные силы бывают сосредоточенными и распределенными.

Р – сосредоточенная сила, Н. Она действует на небольшую часть поверхности тела.

q – интенсивность распределенной нагрузки, Н/м.

Внешние силы могут быть представлены в виде сосредоточенного момента М (Н·м) или распределенного момента m (Н·м/м).

По характеру изменения во времени нагрузки подразделяют на статические и переменные.

Статической называют нагрузку, которая медленно возрастает от нуля до своего номинального значения и остается постоянной в процессе работы детали.

Переменной называют нагрузку, периодически меняющуюся во времени.

Модели разрушения.

Моделям нагружения соответствуют модели разрушения – уравнения (условия), связывающие параметры работоспособности элемента конструкции в момент разрушения с параметрами, обеспечивающими прочность.

В зависимости от условий нагружения рассматривают модели разрушения: статического, малоциклового и усталостного (многоциклового).

Внутренние силы. Метод сечений

Взаимодействие между частями (частицами) внутри элемента конструкции характеризуется внутренними силами.

Внутренние силы представляют собой силы межатомного взаимодействия (связей), возникающие при воздействии на тело внешних нагрузок.

Практика показывает, что внутренние силы определяют прочностную надежность детали (тела).

Для нахождения внутренних сил используют метод сечений. Для этого мысленно рассекают тело на две части, одну часть отбрасывают, другую рассматривают совместно с внешними силами. Внутренние силы распределены по сечению некоторым сложным образом. Поэтому систему внутренних сил приводят к центру тяжести сечения, чтобы можно было определить главный вектор 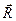и главный момент М внутренних сил, действующих по сечению. Затем раскладываем главный вектор и главный момент на составляющие по трем осям и получаем внутренние силовые факторы сечения: составляющая N_z называется нормальной, или продольной си­лой в сечении, силы Q_x и Q_y называются поперечными силами, момент M_z (или M_к) называется крутящим моментом, а моменты M_х и M_y - изгибающими моментами относительно осей х и y, соответственно.

Таким образом, если внешние силы заданы, то внутренние силовые факторы вычисляются как алгебраические суммы проекций сил и моментов, действующих на мысленно отсеченную часть тела.

После определения числовых значений внутренних сил строят эпюры – графики (диаграммы), показывающие как изменяются внутренние силы при переходе от сечения к сечению.