Касательные напряжения при поперечном изгибе прямого бруса

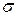При плоском поперечном изгибе, когда в сечениях балки действуют и изгибающий момент М и поперечная сила Q, возникают не только нормальные , но и касательные напряжения .

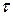Нормальные напряжения при поперечном изгибе рассчитываются по тем же формулам, что и при чистом изгибе:

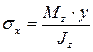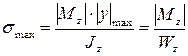;.(6.24)

Далее получим зависимости для определения касательных напряжений в случае поперечного изгиба балки.

Рис.6.11. Плоский изгиб

При выводе формулы примем некоторые допущения:

- касательные напряжения, действующие на одинаковом расстоянии у от нейтральной оси, постоянны по ширине бруса;

- касательные напряжения всюду параллельны силе Q.

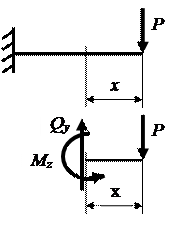
Рассмотрим консольную балку, находящуюся в условиях поперечного изгиба под действием силы Р. Построим эпюры внутренних усилий О_y, и М_z.

На расстоянии x от свободного конца балки выделим элементарный участок балки длиной dx и шириной, равной ширине балки b. Покажем внутренние усилия, действующие по граням элемента: на грани cd возникает поперечная сила Q_y и изгибающий момент М_z, а на грани ab – также поперечная сила Q_y и изгибающий момент M_z+dM_z (так как Q_y остается постоянной по длине балки, а момент М_z изменяется, рис. 6.12). На расстоянии у от нейтральной оси отсечем часть элемента abcd, покажем напряжения, действующие по граням полученного элемента mbcn, и рассмотрим его равновесие. На гранях, являющихся частью наружной поверхности балки, нет напряжений. На боковых гранях элемента от действия изгибающего момента М_z, возникают нормальные напряжения:

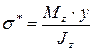; (6.25)

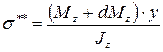. (6.26)

Кроме того, на этих гранях от действия поперечной силы Q_y, возникают касательные напряжения 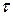, такие же напряжения возникают по закону парности касательных напряжений и на верхней грани элемента.

Составим уравнение равновесия элемента mbcn, проецируя равнодействующие рассмотренных напряжений на ось x:

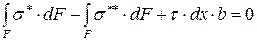, (6.27)

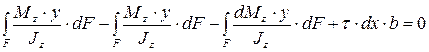, (6.28)

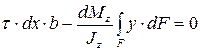. (6.29)

Выражение, стоящее под знаком интеграла, представляет собой статический момент боковой грани элемента mbcn относительно оси x, поэтому можем записать

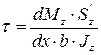. (6.30)

Учитывая, что, согласно дифференциальным зависимостям Журавского Д. И. при изгибе,

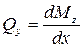, (6.31)

выражение для касательныхнапряжений при поперечном изгибе можем переписать следующим образом (формула Журавского)

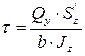. (6.32)

Проанализируем формулу Журавского.

Q_y – поперечная сила в рассматриваемом сечении;

J_z – осевой момент инерции сечения относительно оси z;

b – ширина сечения в том месте, где определяются касательные напряжения;

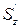– статический момент относительно оси z части сечения, расположенной выше (или ниже) того волокна, где определяется касательное напряжение:

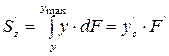, (6.33)

где 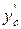и F' – координата центра тяжести и площадь рассматриваемой части сечения, соответственно.