Определение напряжений при косом изгибе

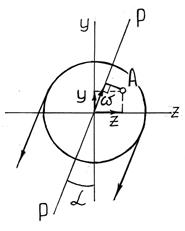
Используя принцип независимости действия сил (принцип суперпозиции) найдем напряжения при косом изгибе. Рассмотрим точку A с координатами (y, z) в сечении изгибаемой балки и определим в ней напряжения от каждого из внутренних усилий, возникающих при косом изгибе:

нормальные напряжения от изгибающего момента M_z

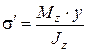; (7.3)

нормальные напряжения от изгибающего момента M_y

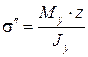; (7.4)

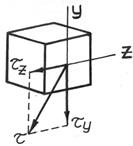
касательные напряжения от поперечной силы Q_y

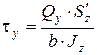; (7.5)

касательные напряжения от поперечной силы Q_z

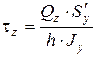(7.6)

Полные напряжения 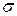и при косом изгибе найдем путем геометрического суммирования составляющих:

а) касательных

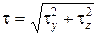; (7.7)

б) нормальных

(7.8)

Последнюю формулу удобно представить в виде

,

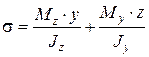или

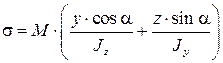, (7.9)

где 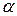– угол наклона силовой плоскости P при косом изгибе (а при сложном изгибе 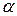– угол наклона плоскости действия полного изгибающего момента M в данном сечении).

7.3 Определение положения нейтральной оси и максимальных
нормальных напряжений при косом изгибе. Условие прочности

Нейтральная ось – линия, во всех точках которой нормальные напряжения равны нулю. При этом в точках сечения, наиболее удаленных от нейтральной оси нормальные напряжения принимают свои экстремальные значения – минимум и максимум.

Заметим, что при плоском изгибе нейтральная ось совпадала с одной из главных осей сечения (Oy или Oz), при косом же изгибе это не так. Выведем формулу для определения положения нейтральной оси при косом изгибе.

Так как 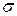=0, то можем записать:

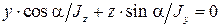
Отсюда найдем уравнение нейтральной оси:

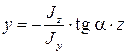(7.10)

Более удобно записать это уравнение через угол 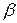наклона нейтральной линии к оси Oz:

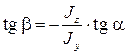(7.11)

Знак «минус» в этой формуле показывает, что углы 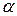и 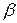откладываются от разноименных осей, но в одном направлении.

Как видим, в случае, когда J_z ≠ J_y, углы 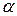и 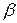не равны друг другу, а, значит, и плоскость кривизны (плоскость максимальных прогибов) бруса не будет совпадать с плоскостью действия сил. Поэтому такой изгиб и назван «косым».

Определим максимальные нормальные напряжения при косом изгибе и запишем условие прочности.

Как известно, нормальные напряжения достигают своих экстремальных значений в точках, наиболее удаленных от нейтральной оси (координаты таких точек обозначим y_max и z_max):

,

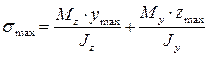или

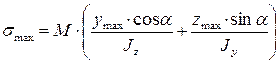(7.12)

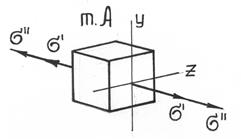
Для прямоугольного сечения – это точки A и B. При M>0 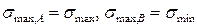(см. рис.7.8).

Для материалов, одинаково сопротивляющихся растяжению (сжатию), максимальные напряжения определяются так:

,

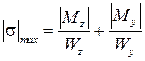или

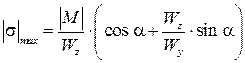, (7.13)

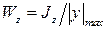где и 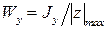– моменты сопротивления сечения относительно осей z и y.

В случае косого изгиба, как правило, проверка прочности осуществляется только по нор-мальным напряжениям (действие касательных невелико). Поэтому условие прочности записывается в виде:

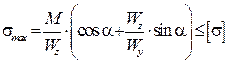(7.14)

При косом изгибе (впрочем, как и при остальных видах нагружения) имеем три задачи расчета на прочность:

- проверка прочности;

- подбор сечения (определить W_z (размеры сечения) при заданном отношении W_z/W_y);

- проверка по несущей способности (определить M).

7.4. Изгиб с кручением. Определение внутренних усилий и
напряжений

Ранее нами был рассмотрен расчет на прочность валов при чистом кручении. Однако круглые валы редко работают на чистое кручение. Как правило, при работе вал изгибается собственным весом, весом шкивов, давлением на зубья шестерен, натяжением ремней и т. д. В таком случае вал будет находиться в условиях сложного сопротивления и испытывать совместное действие кручения и изгиба.

Изгиб с кручением – частный случай сложного сопротивления, который может рассматриваться как сочетание чистого кручения и поперечного изгиба.

P3 P2 P1 P Рис.7.9. Изгиб с кручением

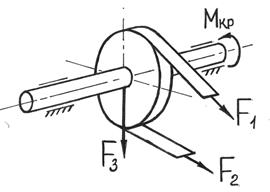
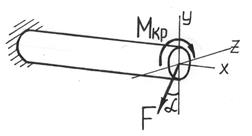
Определение внутренних усилий и напряжений при кручении с изгибом.Для определения внутренних усилий воспользуемся методом сечений:

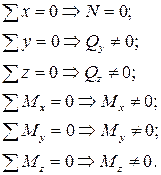(7.15)

Обычно две составляющие попе-речной силы (Q_y, Q_z) и изгибающего момента (M_y, M_z) приводят к их полным результирующим

(7.16)

Заметим, что часто поперечной силой пренебрегают (для достаточно длинных валов) и рассматривают кручение с изгибом как совместное действие крутящего (M_x, M_кр, T) и изгибающего (M_и) моментов.

Опасное сечение вала будем искать, как и прежде, по эпюрам внутренних усилий. При построении эпюр внутренних усилий при кручении с изгибом необходимо иметь ввиду следующие правила:

- эпюры крутящего момента M_x, а также эпюры составляющих поперечной силы Q_y, Q_z и изгибающего момента M_y, M_z строятся с использованием метода сечений;

- результирующая поперечная сила Q может не лежать в плоскости действия результирующего изгибающего момента M_и, а потому между ними уже не будет соблюдаться зависимость Журавского (dM/dx=Q), а, следовательно, и правила проверки эпюр, введенные для плоского изгиба;

- эпюра полного изгибающего момента будет прямой только на тех участках, где M_y и M_z ограничены прямыми с общей нулевой точкой, на участках, где такая общая точка отсутствует эпюра M_и будет описываться вогнутой кривой и строится по точкам (связано с тем, что вектор M_и в разных сечениях имеет различное направление).

Опасное сечение при кручении с изгибом устанавливается из совместного анализа эпюр крутящего M_x и полного изгибающего M_и моментов. Опасным будет считаться то сечение, где оба момента достигают своей максимальной величины. Если моменты достигают максимума в разных сечениях, необходимо проверить все сечения, в которых эти внутренние усилия достаточно велики.

Для определения максимальных напря-жений используем принцип независимости дей-ствия сил и найдем напряжения отдельно от кручения и отдельно от изгиба:

напряжения при кручении

, (7.17) 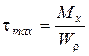; (7.18)

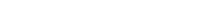напряжения при изгибе

,

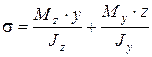или

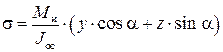, (7.19)

где J_ос – осевой момент инерции для круглого сечения (J_ос = J_z = J_y).

Вводя обозначение 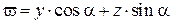, можем записать

, (7.20)

при этом

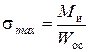, (7.21)

где W_ос – осевой момент сопро-тивления для круглого сечения (W_ос=J_ос/ 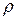_max, 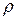_max=d/2).

Опасными точками в сечении будут являться точки наиболее удаленные от нейтральной оси (для круглого сечения – линии, перпендикулярной плоскости действия результирующего изгибающего момента). При этом в токах сечения будет возникать плоское напряженное состояние, а потому расчет на прочность необходимо проводить с привлечением известных теорий прочности.