Методы прямого перебора и динамического программирования
Эти методы являются наиболее точными методами оптимального резервирования. Метод прямого перебора, который сводится к перебору всех возможных решений, является громоздким и редко применяется при проектировании систем. Метод динамического программирования является модификацией метода прямого перебора (алгоритм Кеттеля) [20]. Применительно к задаче оптимального резервирования он сводится к отысканию доминирующей последовательности решений, т.е. последовательности векторов состава системы, включающие все множество оптимальных решений. Будем считать, что один состав системы, представляющий собой некоторую комбинацию расположения резервных элементов, доминирует над другим, если имя одного и того же уровня надёжности обеспечение этого состава связано с наименьшими затратами. Члены доминирующей последовательности обладают тем свойством, что если вектор состава системы X(K) член доминирующей последовательности с показателями надёжности PK и затратами CK, то невозможно найти такой вектор состава X(l), чтобы имели место оба неравенства Pl>PK; Cl£CK. Все неоптимальные решения, не входящие в состав доминирующей последовательности в силу того, что они обладают большей величиной затрат при тех же затратах, чем члены доминирующей последовательности, просто исключаются из рассмотрения. Задача состоит в построении доминирующей последовательности для всей системы, состоящей из “n” подсистем. Для этого берутся две произвольные подсистемы (n-1)-ую и “n”-ую, для которых строится доминирующая последовательность. После построения доминирующей последовательности для “n-1”-ой и “n”-ой подсистемы вся система сводится к системе из 1, 2, …, n-2, (n-1)* подсистем, где (n-1)* - некая условная подсистема, получающаяся в результате композиции подсистем “n” и (n-1). Систематически применяя подобную процедуру, мы через “n” этапов сведём нашу систему, состоящую из “n” подсистем к одной условной подсистеме 1*, для которой будет известна доминирующая последовательность. Требуемый вектор состава резервных элементов X0 выбирается из доминирующей последовательности, исходя из заданных ограничений, т.е. при решении первой задачи оптимального резервирования выбирается такой вектор X0 при котором P(X0)≥P0, а при решении второй – такой, при котором C(X0)£C0.
Для построения доминирующей последовательности для “n-1”-ой и “n”-ой подсистем составляется таблица. Размер таблицы определяется по заданным значениям надёжности или затрат. В таблице: xn-1 и xn число резервных элементов в “n-1”-ой и “n”-ой подсистемах; P(xn-1, xn), С(xn-1, xn) – показатели надёжности и “стоимости” последовательно соединённых на логической схеме “n-1”-ой и “n”-ой системах соответственно при xn-1 и xn резервных элементах.
Таблица №11.1
| xn | xn-1 | |||
| … | ||||
| P(0,0); С(0,0) | P(1,0); С(1,0) | P(2,0); С(2,0) | ||
| P(0,1); С(0,1) | P(1,1); С(1,1) | P(2,1); С(2,1) | ||
| P(0,2); С(0,2) | P(1,2); С(1,2) | P(2,2); С(2,2) | ||
| … |
Доминирующая последовательность строится следующим образом: для прямой задачи из таблицы находится наименьшее значение P1 >P0 (P0 – задано). Если это значение может быть получена с помощью нескольких вариантов, то выбирается вариант с наименьшими затратами C1, а остальные исключаются из рассмотрения. Полученный вектор состава системы с показателями P1 и C1 будет первым членом доминирующей последовательности. Далее из таблицы находится следующий по величине показатель надёжности P2>P1 и аналогично определяется второй член доминирующей последовательности и т.д. Для обратной задачи члены доминирующей последовательности определяются показателю “стоимости”.
Проиллюстрируем алгоритм Кеттеля на примере.
Пример №1.
Передающее устройство состоит из 3х блоков (1, 2, 3). Вероятности отказов блоков за наработку [0, ti] равны Q1(ti)=0,1; Q2(ti)=0,02; Q3(ti)=0,01, а величина затрат на каждый блок: С1=3; C2=2; Q2=1. Определить оптимальный состав устройства, который может быть получен путём нагруженного резерва при условии, что величина отказа устройства за наработку (0, ti) Q(ti)£ Q0(ti)=0.03 при минимальных затратах.
Решение.
Рассмотрим композицию блока 1 и блока 2 и построим для них доминирующую последовательность. В клетках 1, 2, 3 (номера клеток в таблице N2) записываются значения вероятности отказа за наработку (0, ti) – величины Q1(x1) и значения затрат С1(x1) для блока 1 в зависимости от числа резервных элементов x1. В клетках 4, 5, 6 записываются те же значения для блока 2. Эти значения определяются следующим образом:
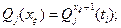
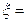 1, 2; j=1, 2;
1, 2; j=1, 2; 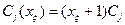
Максимальное число резервных элементов взято равным двум. В случае необходимости размер таблицы может быть увеличен. В клетках 7-15 записаны значения вероятностей отказа за наработку (0, ti) 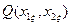 и затрат
и затрат 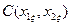 для последовательного соединения блоков 1 и 2 с различным числом резервных элементов, подключенных к каждому из них:
для последовательного соединения блоков 1 и 2 с различным числом резервных элементов, подключенных к каждому из них:
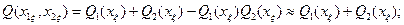
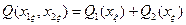
Таблица №11.2
| Число x1 резервных элементов к блоку 1 | |||||
| С1=3; Q1=0.1 | С2=6; Q2=0.01 | С3=9; Q3=0.001 | |||
| Число x2 резервных элементов к блоку 2 | С4=2; Q4=0.02 | С7=5; Q7=0.12 | С8=8; Q8=0.03 | С9=11; Q9=0.021 | |
| С5=4; Q5=0.0004 | С10=7; Q10=0.1 | С11=10; Q11=0.01 | С12=13; Q12=0.0014 | ||
| С6=6; Q6=0.000008 | С13=9; Q13=0.1 | С14=12; Q14=0.01 | С15=15; Q15=0.001 |
Первый член доминирующей последовательности для композиции блоков 1 и 2 находится в клетке 8 таблицы №2. ему соответствует максимально допустимое значение вероятности отказа, равное Q0(ti)=0,03. Векторы состава устройства, расположенные в клетках 7, 10, 13 имеют значение вероятности отказа больше чем Q0(ti). Второй член – в клетке 11: он обладает следующим меньшим значением 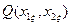 . Векторы состава устройства, расположенные в клетках 9 и 14, исключаются из рассмотрения, так как они имеют такое же и большее значение
. Векторы состава устройства, расположенные в клетках 9 и 14, исключаются из рассмотрения, так как они имеют такое же и большее значение 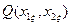 , чем у второго члена при больших затратах. Третий член доминирующий последовательности расположен в клетке 12, а четвёртый – в клетке 12. Остальные члены исключаются, т.к. имеют ненадёжность большую, чем заданная Q0(ti).
, чем у второго члена при больших затратах. Третий член доминирующий последовательности расположен в клетке 12, а четвёртый – в клетке 12. Остальные члены исключаются, т.к. имеют ненадёжность большую, чем заданная Q0(ti).
Далее строится таблица №3, в которую заносятся значения полученной доминирующей последовательности (клетки 1, 2, 3, 4) и значения Q3(x3) и С3(x3), полученные аналогично предыдущему для блока 3.
Таблица №11.3
| Число x1 и x2 резервных элементов, подключенные к блокам 1 и 2 | ||||||
| x1= 1 x2 =0 | x1= 1 x2 =1 | x1= 2 x2 =1 | x1= 2 x2 =2 | |||
| С1=8; Q1=0.03 | С2=10; Q2=0.01 | С3=13; Q3=0.0014 | С4=15; Q4=0.001 | |||
| Число x3 резервных элементов, подключённых к блоку 3 | С5=1; Q5=0.01 | С8=9; Q8=0.04 | С9=11; Q9=0.02 | С10=14; Q10=0.011 | С11=16; Q11=0.011 | |
| С6=2; Q6=0.0001 | С12=10; Q12=0.03 | С2=12; Q2=0.01 | С14=15; Q14=0.0015 | С15=17; Q15=0.0011 | ||
| С7=3; Q7=0.000001 | С16=11; Q16=0.03 | С2=13; Q2=0.01 | С16=16; Q16=0.0014 | С19=18; Q19=0.001 |
Таким образом в клетках 8-19 записаны вероятности отказов за время (0, ti) устройства 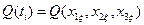 и затрат
и затрат 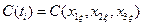 при различном числе резервных элементов, подключённых к каждому из основных. Просматривая все значения
при различном числе резервных элементов, подключённых к каждому из основных. Просматривая все значения 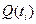 , приведённые в таблице N3, находим требуемый вектор состава системы, который имеет
, приведённые в таблице N3, находим требуемый вектор состава системы, который имеет 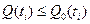 и минимальное значение затрат. Этот вектор состава находится в клетке 12 – в ней приведены значения
и минимальное значение затрат. Этот вектор состава находится в клетке 12 – в ней приведены значения 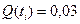 и С=10. При этом к блокам 1 и 3 подключается по одному резервному элементу.
и С=10. При этом к блокам 1 и 3 подключается по одному резервному элементу.
Вектор оптимального состава:
x1=1; x2=0; x3=1, при этом Q=0,03, С=10=min.
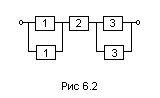
Логическая схема устройства, обеспечивающая 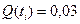 при С=10=min представлена на рис 11.2
при С=10=min представлена на рис 11.2
|
Дата добавления: 2016-09-26; просмотров: 4154;











