Резервирование элементов, отказывающих по причине обрыва или короткого замыкания

При резервировании в этом случае вероятность безотказной ра­боты элемента" р необходимо рассматривать как содержащую две составляющие р₁ и р₂, соотношение между которыми зависит от типа элементов. Например, отказ диода может вызвать обрыв или короткое замыкание в блоке. Структурная схема надежности блока с учетом обрыва и короткого замыкания представлена на рис. 9.9.

Рис. 9.9. Структурная схема надежности блока

Если вероятность безотказной работы относительно обрыва p₂ а вероятность безотказной работы относительно короткого замыка­ния — р₂, то тогда вероятность безотказной работы диода p=p₁p₂.

Пусть блок дублируется. Для наглядности блок будем пред­ставлять в виде диода (рис. 9.11). Тогда вероятность повреждения в связи с обрывом уменьшается, так как повреждение возникает при обрыве в обоих диодах, а при коротком замыкании возрастает, так как достаточно, чтобы произошло короткое замыкание хотя бы одного из диодов. В этом случае струк­турная схема надежности имеет вид, предста­вленный на рис. 9.12. Если блоки соединены последовательно (рис. 9.13), то получается схема надежности, изоб­раженная на рис. 9.14, с параметрами которой можно оперировать, как с элементами. Вероятность безотказной работы схемы, данной на рис. 9.11, имеет вид

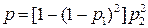, (9.33)

а вероятность безотказной работы схемы, представленной

на рис. 9.14, будет

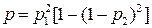. (9.34)

Рассмотренные примеры позволяют сделать выводы: 1. Парал­лельное и последовательное соединение элементов в принципиаль­ных схемах не всегда соответствуют параллельному и последова­тельному соединению в схемах по надежности. 2. Надежность работы

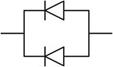
Рис. 9.10. Дублированный блок

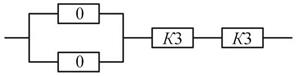
Рис. 9.11. Структурная схема надежно­сти дублированного блока

элементов зависит от ряда параметров. При расчете нужно разли­чать параметры типа «О» (обрыв), надежность которых повышается посредством

параллельного включения аналогичных элементов, и параметры типа «КЗ» (короткое замыкание), надежность которых повышается при последовательном соединении элементов.

Рис. 9.12. Последователь­ное соединение

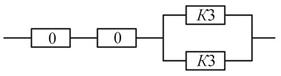
Рис. 9.13. Структурная схема надежно­сти последовательного соединения

Следует рассмотреть выигрыш надежности при s-кратном резер­вировании. Структурная схема надежности элемента при кратности резервирования s—1 показана на рис. 9.14. В этом случае вероят­ность безотказной работы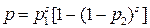

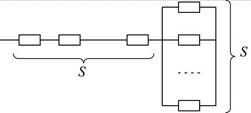
Рис.9.14. Структурная схема надежности группы с кратностью резервирования

Отсюда видно, что если второй сомножитель с ростом s стре­мится к единице, то первый убывает, поэтому максимальная на­дежность обеспечивается при некотором определенном р, величина которого зависит от, соотношенияp_iи р₂. Исследование этого урав­нения показывает, что максимум функции р(х) достигается при

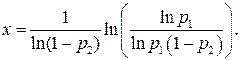
Действительно

.

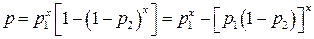Притом, что

.

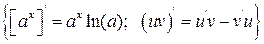Тогда

.

;

;

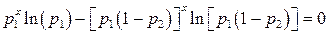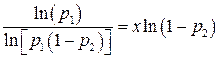Следовательно

.

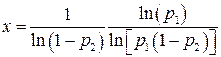В качестве sнеобходимо брать ближайшее к х целое число, дающее большее значение для р. Если p₁=p₂,то р=р₁^s[1—(1—Pi)^s].

Так как р₁²>р₁^s[1—(1—Pi)^s],то при s> 2 повысить надеж­ность не удается. Если соединить элементы одним из двух способов, пред­ставленных на рис.9.16 а,б, то структурные схемы их параметров надежности будут иметь ВИД, изображенный на рис.9.15, в,г. Из схем видно, что последовательно-параллельное соединение соответствует блочному резервированию другого параметра. На рис. 9.15 в структурная схема по короткому замыканию соответствует раздельному резервированию, поэтому на рис. 9.15, в, г следует

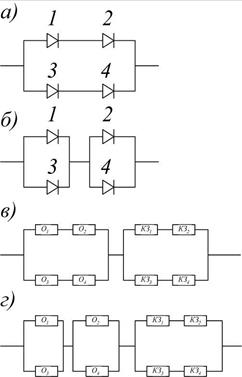
Рис. 9.15. Последовательно-парал­лельное резервирование (а) и струк­турная схема надежности для парал­лельно-последовательного резервиро­вания (б)

читать 0₁—0₂; О₃—0₄; К<3₁—К3₃;К3₂—КЗ_9. В обоих случаях вероят­ность безотказной работы

Если имеется s элементов в цепочке и j цепочек, то

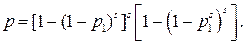
Вероятность безотказной работы параметров типа «О» и «КЗ» соответственно равна 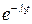и .

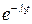Если известно, какая доля от общего числа отказов вызвана отказом типа «КЗ» и «О», то 𝜆₁ =Ь и𝜆₂= (1—b)𝜆, где Ь—доля отказов по причине короткого замыкания Следо­вательно, 𝜆=𝜆₁+𝜆₂.

Зависимость вероятности без­отказной работы элементов от спо­собов резервирования дана в табл. 9.1. В ней элементы разде­лены на три группы: I группа элементов выходит из строя из-за отказов типа «О» и «КЗ»; II — из-за отказов типа «О»; III — из-за отказов типа «КЗ».

Таблица 9.1.

Способ резервирования	Группы элементов
I	II	III
Без резервирования	p1p2	p1	p2
Последовательный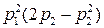
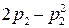
Параллельный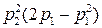
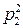
Последовательно- параллельный Параллельно-последовательный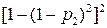

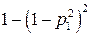
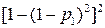
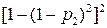
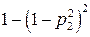
При определении надежности схем, приведенных на рис. 9.9 и 9.12, предполагалось, что появление короткого замыкания (или обрыва) не зависит от того, работоспособен или нет рассматривае­мый элемент. В действительности характер зависимости надежности более сложный. Например, для схемы, показанной на рис. 9.12, которая реализуется по отказу типа «КЗ», целесообразно различить обрыв у работоспособного элемента и элемента, который замкнут накоротко. Для схемы, представленной на рис, 9.9, необходимо различить вероятность появления короткого замыкания у работоспособного элемента и элемента, который уже отказал из-за обрыва.

Метод свертки

В общем случае устройства и системы с резервиро­ванием представляют собой сложные последовательно-параллельные структуры. При расчете надежности таких устройств используют метод, позволяющий перейти к структуре последовательно соединенных элемен­тов. Метод основан на замене нескольких параллельно соединенных эле­ментов структуры одним элементом с эквивалентной надежностью, учитывающей параллельность соединения. Таким образом, сложная структура постепенно «сворачивается» в простую последовательную. Поэтому такой метод и называется методом свертки.

Проиллюстрируем метод с помощью сворачивания структуры, изо­браженной на рис. 9.16, а. Обозначим вероятности безотказной работы структурных элементов У1, У2, ..., У11 за некоторое время t, как P₁, P₂, …, P₁₁ а вероятности их отказов Q₁, Q₂, …, Q₁₁ соответственно. Вы­делим узлы, состоящие из параллельно соединенных элементов: узел 1 - элементы УЗ, У4, У5; узел 2 - элементы У7, У8; узел 3 - элементы У9, У10, У11. Найдем вероятности отказа этих узлов:

.

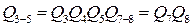
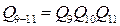Вероятность их безотказной работы соответственно будет:

.

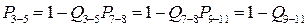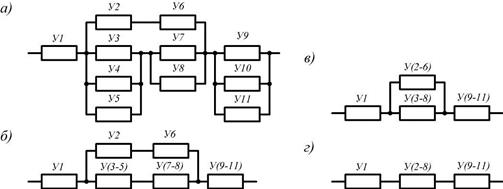
Рис. 9.16. Принцип сворачивания структуры системы

Осуществим первую свертку в структуре, заменив узлы 1, 2, 3 эквива­лентами с вероятностями безотказной работы 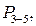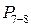, 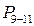. Трансфор­мированная структура изображена на рис. 9.16, б. Она содержит один узел, состоящий из двух параллельных ветвей: ветвь 1 - элементы У2, У6, ветвь 2 - элементы У (3-5), У(7-8). Вероятности безотказной работы этих ветвей:

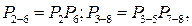
а вероятности отказа:

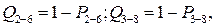
Осуществим вторую свертку, за­меняя ветвь 1 и ветвь 2 эквивалента­ми с вероятностями отказа 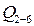, 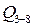В новой структуре (рис. 9.16, в) имеется лишь один узел, веро­ятность отказа которого 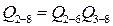, а вероятность без­отказной работы соответствен­но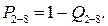

Осуществляем третью свертку, заменяя узел У(2-6), У(3-8) эквива­лентом с вероятностью безотказной работы . В результате приходим к простой последовательной струк­туре (рис. 9.16, г). Таким образом, вероятность безотказной работы системы с исходной структурой (рис. 9.16, а) может быть определена как 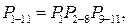вероятность отказа соответственно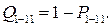

В некоторых случаях не удается непосредственно с помощью метода свертки перейти к простой последовательной структуре. Это относится к сложным структурам с перекрестными связями. Для них применяют дру­гие методы, рассматриваемые далее.