Показатели надежности устройств с постоянным нагруженным резервом

На рис. 9.2, а представлена структура некоторой системы с резервиро­ванием в виде схемы соединений основных и резервных элементов (функ­циональных узлов, блоков). Она состоит из n основных элементов, каж­дый из которых, кроме У12, резервируется со своей кратностью – K_р. Для элемента У12 нет резерва, то есть для него К_р=0. Для определенности бу­дем предполагать, что резервирование постоянное.

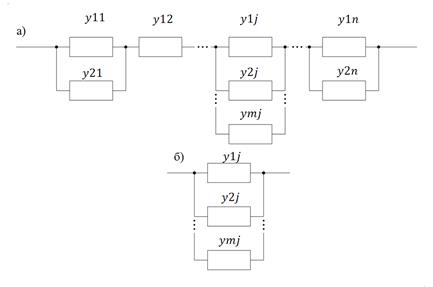
Рис. 9.2. Структура системы с резервированием: а – Обобщенная структура, б – узел структуры.

Как следует из рис. 9.2, а, чтобы найти показатель надежности устройст­ва в целом, прежде всего надо определить показатели надежности узлов из параллельно соединенных основного и резервных элементов (рис. 9.2, б).

Пусть резервные элементы, как и основной, являются нагруженными. В этом случае основной и резервные элементы можно считать равнонадежными с вероятностью безотказной работы Pj(t) и вероятностью отказа Q_j(t). Тогда вероят­ность отказа j-го узла из т ветвей, то есть с кратностью резервирования 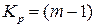, будет равна:

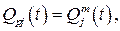(9.1)

а вероятность безотказной работы

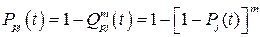. (9.2)

Воспользовавшись (9.2) и (1.2), определим в общем виде плотность ве­роятности отказа j -го узла:

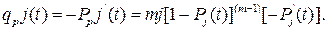
Принимая во внимание, что 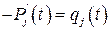окончательно получим

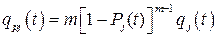(9.3)

Опираясь на (9.2) и (9.3), найдем интенсивность отказов j-го узла:

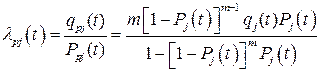. (9.4)

В выражении (9.4) 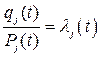интенсивность отказов любого из элементов j-го узла. Таким образом:

(9.5)

Предположим что 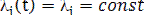, что отвечает математической модели

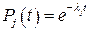(9.6)

Пусть 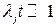, тогда

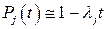. (9.7)

После подстановки (9.7) в (9.5)

.

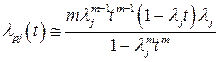Учитывая, что , окончательно получим

. (9.8)

Как следует из (9.8), при m=const и λ_i=const интенсивность отказов j-го узла 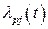со временем монотонно возрастает и тем быстрее, чем больше кратность резервирования. Это говорит о том, что с точки зрения надеж­ности узел является стареющим. Рассмотрим для иллюстрации три част­ных случая.

1. Резервирование отсутствует: т=1, К_р=О,

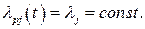
2. Однократное резервирование (дублирование):

m=2, K_p=l,

.

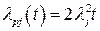3. Двукратное резервирование: m=3, K_p=2,

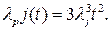
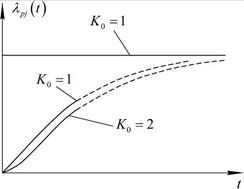
Рис. 9.3. Зависимость интенсивности отказов от времени при различной кратности резервирования

Для рассмотренных случаев функции λ_i(t) отображены на рис. 9.9. Важно отмстить, что для узла с резервированием всегда 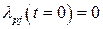. Это говорит об абсолютной надеж­ности узла в момент времени t=0. Действительно, в этот момент одновре­менно не могут отказать два и более элементов, а только один, что не мо­жет привести к отказу узла в целом. Найдем формулу, определяющую среднюю наработку j-го узла с резервированием 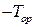,Исходя из (1.4) мо­жем записать:

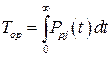
или, используя (9.2) и (9.6),

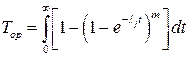(9.9)

Воспользуемся методом математической индукции для перехода от формулы (9.9) к другой, более удобной и наглядной. Для этого последова­тельно найдем значение интеграла при m=1, m=2, m= 3 и.т.д. (индекс j опускаем):

При m = 1

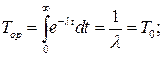
При m = 2

;

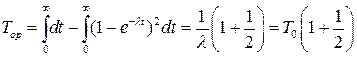При m = 3

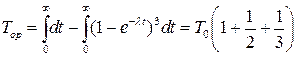
и т. д. Выявляется закономерность, которая позволяет для произвольного числа ветвей m записать:

.

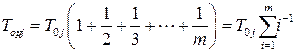Таким образом, найдены формулы для определения всех основных по­казателей надежности узла с резервированием через показатели надежно­сти первичного элемента в случае нагруженного резерва. Имея в виду, что для устройства, приведенного на рис. 9.2, а, соединение узлов последова­тельное, находим вероятность безотказной работы устройства:

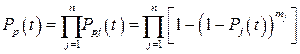. (9.11)

При проектировании устройств или систем со структурным резервиро­ванием приходится решать следующую задачу. Исходно известны вероят­ность безотказной работы P(t) или вероятность отказа Q(t) основного и ре­зервных элементов. Задана вероятность безотказной работы или вероятность отказа Q_p(t), которые должны быть обеспечены путем приме­нения резервирования. Требуется определить достаточную для этого крат­ность резервирования К_р= m-1. Такой постановке задачи соответствует рис. 9.2, б. Для ее решения используем формулы (9.1) и (9.2), опуская индекс j. Формулу (9.2) представим в виде

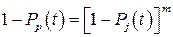. (9.12)

После логарифмирования (9.1) и (9.12) находим m как целое число:

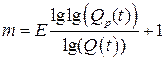, (9.13)

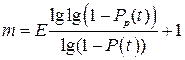, (9.14)

где Е - оператор взятия целой части числа. Учитывая, что К_р=т-1, из (9.13) и (9.14) получаем

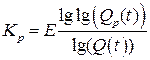, (9.15)

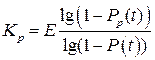. (9.16)

Пример. Требуется обеспечить с помощью резервирования вероят­ность отказа устройства 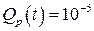при вероятности отказа без резерви­рования 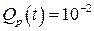. Применяя (9.15), находим

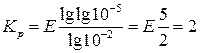или .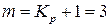

9.3. Показателинадежности при резервированиис ненагруженным резервом

Пусть имеется некоторая система (рис. 9.5) из m одинаковых уст­ройств. В этой системе устройство У1 назовем основным, остальные (m-1) - резервными. Пока основное устройство работоспособно, резерв­ные находятся в ненагруженном состоянии. Предполагается, что в этом состоянии они абсолютно надежны.

При обнаружении отказа основного устройства его замещает любое из (m-1) резервных. Так происходит при каждом очередном отказе, пока не будут использованы все (m-1) резервные устройства. Продолжительность работоспособного состояния такой системы определяется суммой:

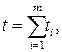
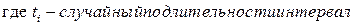
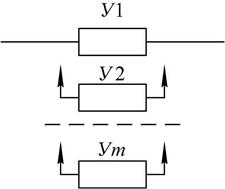
Рис. 9.4. Резервирование замещением времени работоспо­собного состояния i-го устройства системы от момента его подключения до отказа.

Для случая экспоненциальной модели веро­ятности безотказной работы каждого из уст­ройств 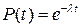в [3] показано, что вероят­ность безотказной работы системы (рис. 9.5) будет определяться зависимостью

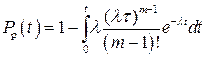. (9.23)

Если в (9.25) осуществить замену 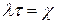, то выражение примет вид

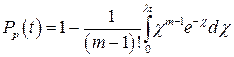(9.24)

Учитывая, что, по определению,

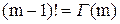, (9.25)

(9.26)

это Г- функции, окончательно получим

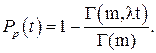(9.27)

Значение Г-функций от их аргументов приведены таблично в справочниках.

В частности, решая интегральное уравнение (9.22) для случая m=2, по­лучим

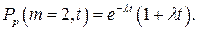(9.28)

Тогда средняя наработка до отказа для этого случая

В общем же случае при произвольном m:

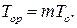(9.29)

Из сопоставления соотношения (9.29) с (9.10) следует, что использование резервирования с ненагруженным резервом даст значительный выиг­рыш по средней наработке до отказа по сравнению со случаем нагружен­ного резерва.