Сопоставление общего и раздельного резервирования
Пока не затрагивался вопрос о предпочтительности общего или раздельного резервирования с точки зрения обеспечения лучших показателей надежности ЭУ. Для сопоставления упомянутых разновидностей резервирования по эффективности предположим, что имеется некоторое ЭУ, состоящее из п основных равнонадежных элементов (рис. 9.4). Вероятность безотказной работы одного элемента - P(t), а вероятность отказа - Q(t). Пусть как при общем, так и при раздельном резервировании кратность резервирования одна и та же: 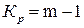 . Найдем вероятность безотказной работы ЭУ с общим резервированием (рис. 9.4, а):
. Найдем вероятность безотказной работы ЭУ с общим резервированием (рис. 9.4, а):
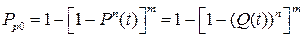 (9.17)
(9.17)
с раздельным резервированием
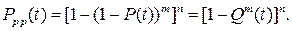 (9.18)
(9.18)
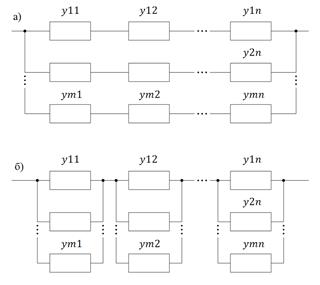
Рис. 9.3. Структура систем: а – с общим резервированием, б – с резервным
Принимая во внимание, что вероятность отказа Q(t)«1, можно воспользоваться приближенными равенствами:
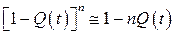 (9.19)
(9.19)
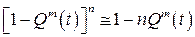 . (9.20)
. (9.20)
В левой части (9.19), (9.20) стоит известное выражение бинома Ньютона, а в правой - два старших члена разложения бинома в ряд. Таким образом, будут справедливы приближенные равенства:
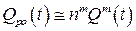 , (9.21)
, (9.21)
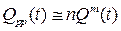 , (9.22)
, (9.22)
Откуда 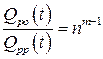 .
.
Как видим, для рассматриваемого случая вероятность отказа ЭУ с общим резервированием в 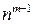 раз больше, чем с раздельным. Это позволяет сделать вывод о предпочтительности раздельного резервирования по сравнению с общим с точки зрения повышения надежности ЭУ.
раз больше, чем с раздельным. Это позволяет сделать вывод о предпочтительности раздельного резервирования по сравнению с общим с точки зрения повышения надежности ЭУ.
9.5. Скользящее резервирование
Как уже было определено в подразд. 9.1, скользящее резервирование используется для нескольких одинаковых элементов системы, например микропроцессоров. При этом любой отказавший из п основных элементов может быть заменен любым из m резервных. Система окажется в неработоспособном состоянии, если при очередном отказе окажутся исчерпанными резервные элементы.
Если интенсивность отказов основных и резервных элементов одинакова, то при экспоненциальной модели вероятность безотказной работы системы, содержащей и основных и т резервных элементов, в режиме нагруженного
резерва можно определить по формуле [11]
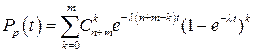 (9.30)
(9.30)
Средняя наработка до отказа при этом определяется зависимостью
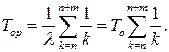 (9.31)
(9.31)
Для случая не нагруженного резерва
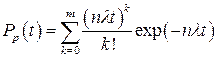 (9.32)
(9.32)
и
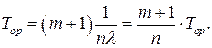 (9.33)
(9.33)
9.6. Резервирование с применением мажоритарного элемента
Мажоритарный элемент позволяет обеспечить режим одновременного штатного функционирования основного и резервных элементов ЭУ и исключает применение специальных коммутационных узлов, устраняющих взаимное влияние основного и резервных элементов друг на друга. При этом отказ основного или резервного элементов не влияет на работу оставшихся исправных элементов. В настоящее время весьма широко распространено структурное резервирование с мажоритарным элементом; оно используется для повышения надежности цифровых электронных устройств и цифровых систем.
Мажоритарный элемент - это логическое устройство с нечетным числом входов т=2к+1 (где к = 1,2,9... ) и одним выходом. Чаще всего используются элементы с т = 3, реже с т = 5 и совсем редко с m = 7. Условное обозначение мажоритарных элементов с т=3, т=5 приведено на рис. 9.6, а. Мажоритарный элемент может быть выполнен в виде отдельной микросхемы или собран из нескольких логических микросхем. В дальнейшем для краткости будем называть резервирование с применением мажоритарного элемента просто мажоритарным.
Принцип мажоритарного резервирования поясним на примере с помощью рис. 9.6, б, отображающего часть некоторой цифровой системы. С выхода цифрового устройства У1 цифровые сигналы в виде последовательности символов «0» и «1» поступают на входы трех работающих одновременно одинаковых равнонадежных устройств У21, У22, У23, образующих резервированный узел.
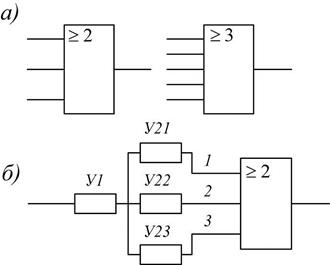
Рис. 9.6. Мажоритарный элемент. а – обозначение элемента, б – подключение к элементу
Цифровые сигналы с выхода каждого из устройств У21, У22, У23 поступают на соответствующий вход мажоритарного элемента (в данном случае трех-входового).
Если каждое из устройств У21, У22, У23 исправно, то в данный момент времени на их выходах будет один и тот же двоичный символ (0 или 1 ), а значит и на входах мажоритарного элемента. Тогда и на выходе мажоритарного элемента будет такой же двоичный символ. Если какое-либо из устройств У21, У22, У23 отказало, то только на двух входах мажоритарного элемента в данный момент времени двоичные символы будут одинаковыми.
На выходе же мажоритарного элемента будет двоичный символ, совпадающий с символом на выходе двух исправных устройств. То есть мажоритарный элемент выполняет логическую операцию принятия решения «по большинству» (операцию «голосования»). Теперь становится понятным, почему число входов у мажоритарного элемента должно быть нечетным и больше единицы. На рис. 9.7 изображена структура трехвходового мажоритарного элемента, из которой становится понятной и логика его работы, отвечающая логической функции Z=(x1⋀x2)⋁(x2⋀x3)⋁(x1⋀x3) Найдем зависимость вероятности безотказной работы узла с мажоритарным резервированием 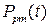
 от вероятности безотказной работы резервируемого и резервных элементов P(t). Начнем с частного случая, отвечающего трехвходовому мажоритарном элементу (рис. 9.6). Предполагаем при этом, что сам мажоритарный элемент абсолютно надежен.
от вероятности безотказной работы резервируемого и резервных элементов P(t). Начнем с частного случая, отвечающего трехвходовому мажоритарном элементу (рис. 9.6). Предполагаем при этом, что сам мажоритарный элемент абсолютно надежен.
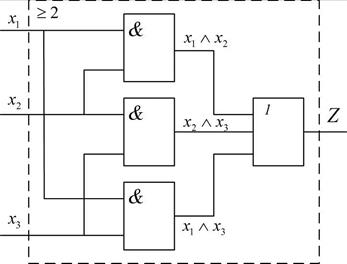
Рис.9.6.Структура мажоритарного элемента
Узел на рис. 9.7 будет работоспособным, если он находится в следующих двух состояниях.
Состояние 1. Работоспособны и У1, и У2, и УЗ. Вероятность нахождения узла в таком состоянии
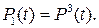 (9.34)
(9.34)
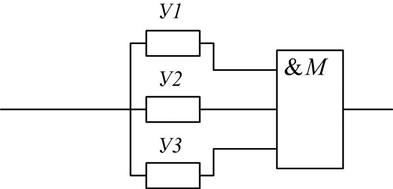
Рис. 9.7. Резервирование с трехходовым мажоритарным элементом.
Состояние 2. Работоспособны два устройства из У1, У2, У9. Вероятность такого состояния
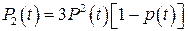 . (9.35)
. (9.35)
Во всех прочих состояниях узел на рис. 9.8 будет в отказе.
Таким образом, вероятность безотказной работы узла определяется суммой:
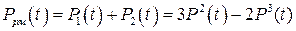 (9.36)
(9.36)
Рассуждая аналогично, можно найти 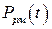 при
при 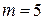 ,
, 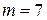 и т.д.
и т.д.
В общем случае зависимость 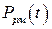
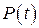 от имеет вид
от имеет вид
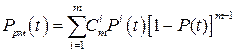 , (9.37)
, (9.37)
Где 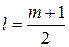 ,
, 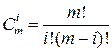 – число сочетаний из
– число сочетаний из 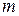 по
по 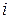 .
.
На рис. 9.9 показано семейство функций 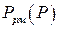 , построенных с использованием (9.37) при
, построенных с использованием (9.37) при 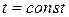 и различных
и различных 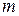 . Анализ поведения этих функций позволяет сделать важный вывод, что мажоритарное резервирование дает положительный эффект, пока
. Анализ поведения этих функций позволяет сделать важный вывод, что мажоритарное резервирование дает положительный эффект, пока 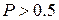 , в противном случае надежность устройства понижается.
, в противном случае надежность устройства понижается.
Устройства с мажоритарным резервированием, как и с любым другим, являются стареющими с точки зрения надежности, то есть интенсивность отказов таких устройств со временем растет.
Среднюю наработку 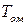 узла с мажоритарным резервированием в общем случае с помощью формулы
узла с мажоритарным резервированием в общем случае с помощью формулы 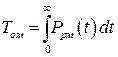 определить затруднительно. Найдем
определить затруднительно. Найдем 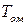 для часто встречающегося случая при
для часто встречающегося случая при 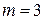 и
и 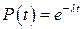 .
.
Воспользуемся при нахождении 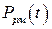 общей формулой (9.37) или ее частным случаем (9.36):
общей формулой (9.37) или ее частным случаем (9.36): 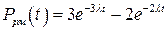 . Тогда
. Тогда
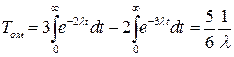 или
или 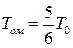 . (9.40)
. (9.40)
Как следует из (9.38), 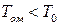 , что является, на первый взгляд, неожиданным.
, что является, на первый взгляд, неожиданным.
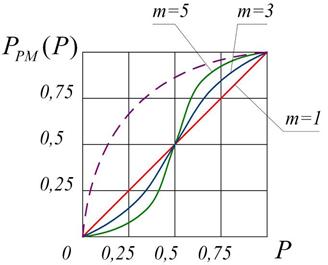
Рис. 9.8. Зависимость вероятности безотказной работы системы от вероятности безотказной работы элемента.
Уменьшает ли резервирование среднюю наработку? Ответ следует искать в «особенности старения» узла с мажоритарным резервированием.
На практике нельзя считать мажоритарный элемент абсолютно надежным. Он обладает известной вероятностью безотказной работы 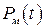 . При расчете надежности это обстоятельство учитывается включением мажоритарного элемента последовательно за резервируемым узлом. Тогда формула (9.37) с учетом надежности самого мажоритарного элемента трансформируется в иную:
. При расчете надежности это обстоятельство учитывается включением мажоритарного элемента последовательно за резервируемым узлом. Тогда формула (9.37) с учетом надежности самого мажоритарного элемента трансформируется в иную:
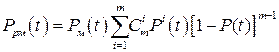 . (9.39)
. (9.39)
Сопоставим по надежности мажоритарное резервирование с обычным постоянным. При сопоставлении в качестве показателей надежности используем вероятности отказов узлов с резервированием 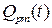 и
и 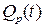 . Сопоставление осуществим для случая, когда
. Сопоставление осуществим для случая, когда 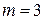 и
и 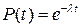 .
.
В соответствии с (9.35) и (9.11) найдем вероятности безотказной работы узлов:
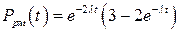 , (9.40)
, (9.40)
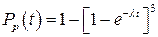 . (9.41)
. (9.41)
Принимая во внимание, что при 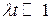 ,
, 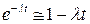 , из (9.40), (9.41) после преобразования получаем
, из (9.40), (9.41) после преобразования получаем
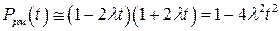 , (9.42)
, (9.42)
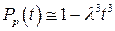 (9.43)
(9.43)
Из (9.42), (9.43) следует, что 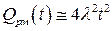 ,
, 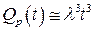 откуда
откуда
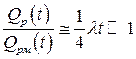 , то есть
, то есть 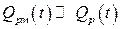 .
.
Таким образом, мажоритарное резервирование, достаточно просто конструктивно реализуется в цифровых устройствах и системах, но значительно уступает по повышению надежности резервированию без мажоритарного элемента. Это объясняется тем, что при обычном резервировании узел остается работоспособным до тех пор, пока не откажут все резервные элементы. При мажоритарном отказ узла происходит уже в том случае, если отказали только 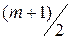 элементов из
элементов из 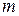 , а остальные еще работоспособны (например, из пяти элементов два). То есть в смысле использования возможностей резерва мажоритарное резервирование далеко от оптимального. Это в полной мере подтверждает характер пунктирной кривой на рис. 9.9, которая отображает зависимость вероятность вероятности безотказной работы устройства пари его двукратном резервировании без мажоритарного элемента.
, а остальные еще работоспособны (например, из пяти элементов два). То есть в смысле использования возможностей резерва мажоритарное резервирование далеко от оптимального. Это в полной мере подтверждает характер пунктирной кривой на рис. 9.9, которая отображает зависимость вероятность вероятности безотказной работы устройства пари его двукратном резервировании без мажоритарного элемента.
Дата добавления: 2016-09-26; просмотров: 2977;











