Задание гамма-процентных ресурсов.

Если долговечность характеризуется двумя видами ресурсов (числом R₁ включений в рабочее состояние и объемом R₂ полезной работы, выполненной во включенном состоянии), то из формул (4.11), (4.12) следует, что существует множество решений в виде пар значений R_1g и R_2g, которые на плоскости наработок образуют линию гамма-процентных ресурсов (рис. 4.2).

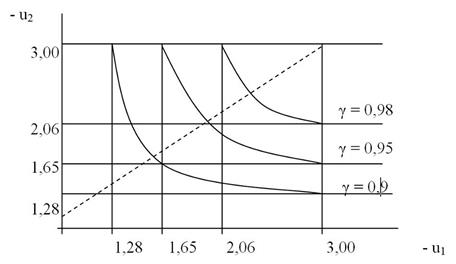
Рис . 4.2. Лини гамма - процентных ресурсов

При известных значениях величин b₁t, b₂t, c₁t, c₂t, a и g построение линии гамма-процентных ресурсов сводится к заданию с некоторым шагом значений R_1g и подбору из соотношения (4.12) соответствующих им значений R_2g.

Так на рис. 4.2 в координатах аргументов u_1, u₂ функции Лапласа построена линия гамма-процентных ресурсов для значений g, равных 90, 95, 98%. В этом случае определение значений R_1g и R_2g сводится к выбору точки на соответствующей линиии гамма-процентных ресурсов, определению ее координат u_1, u₂ и решению системы уравнений вида

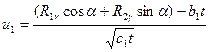; (4.19)

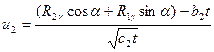(4.20)

относительно R_1g, R_2g, при заданных значениях a, b₁, b_2, c₁, c_2, t.

В некоторых случаях для устранения неопределенности в выборе точки на линии гамма-процентных ресурсов можно использовать ограничения, накладываемые на R_1g, R_2g, Одним из наиболее распространенных ограничений являются ограничения стоимостного типа, например,

C = c₁R_1γ +c₂R_2γ ; (4.21)

откуда R_1γ = 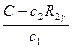, (4.22)

где C – объем ассигнований, выделенных на обеспечение долговечности

объекта;

С₁, С₂ – соответствующие значения стоимости единицы ресурса первого и

второго типа.

Тогда решение поставленной задачи сводится к выбору на линии гамма-процентных ресурсов (рис. 4.2) такой точки, координаты которой R_1g, R_2g, удовлетворяют накладываемым ограничениям.

В п. 4.2 показано, что суммарная наработка объекта 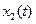при любых законах распределения наработки при каждом включении при достаточно большом числе циклов включений-отключений будет асимптотически нормальна к моменту 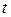с числовыми характеристиками [2,8]

(4.23)

,

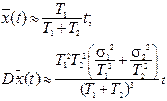где 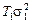-среднее значение и дисперсия наработки объекта при единичном включении;

-среднее значение и дисперсия интервалов между включениями объекта

В частности, если наработки при единичном включении и интервалы между включениями подчинены экспоненциальным законам распределения

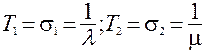, то формулы (4.5) примут вид

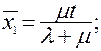
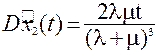. (4.24)

Таким образом, при больших t вероятность того, что суммарная наработка объекта 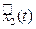превысит значение 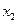на основании формулы (4.8) определится следующим образом

(4.25)

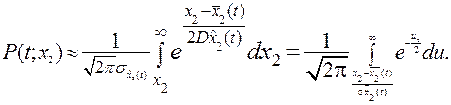
Пример. Требуется найти вероятность того, что за время 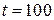ч. наработка объекта 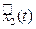превысит заданное значение 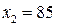ч, если законы наработки при единичном включении и интервалов между включениями являются показательным с параметрами λ=0.1 ч^-1, µ=1 ч^-1 соответственно. Тогда на основании формулы (4.23)

(4.26)

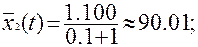
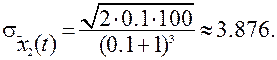
Подстановка полученных значений (4.26) в формулу (4.25) даёт следующее значение вероятности выработки ресурса объекта 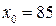ч. за время 100 ч.

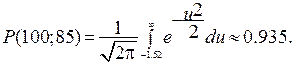
Следует отметить, что любой элемент, прошедший предварительную тренировку (этап 1 жизненного цикла, см. Рис. 2.3, 3.4) может быть условно представлен в виде двух элементов, соединённых последовательно. Надёжность одного элемента будет определяться только старением, другого - только внезапными отказами. Общая безотказность данного объекта состоящего из этих двух условных элементов будет определяться формулой

.

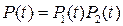Подстановка значени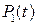й и 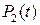из выражений (2.24), (2.43) в эту формулу приводит к следующему результату

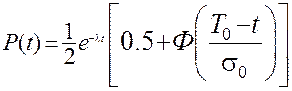. (4.27)