Показатели ремонтопригодности

Под ремонтопригодностью понимается свойство объекта, заключающееся в приспособленности к поддержанию и восстановлению работоспособного состояния путем технического обслуживания и ремонта [1,6,13,14].

В данном случае поддержание и восстановление работоспособности зависит от приспособленности объекта к обнаружению причин возникновения отказов и, естественно, от квалификации персонала.

Для обеспечения хорошей ремонтопригодности объектов в их конструкции предусматривают разъемы, люки, легкосъемные блоки, встроенные элементы контроля и др. Мероприятия такого характера ведут к уменьшению времени и затрат средств, потребных для проведения ремонтов и обслуживания.

Вполне очевидно, что эти средства и время зависят не только от ремонтопригодности объекта, но и от ряда организационных факторов (количества и квалификации специалистов, оснащения рабочих мест, организация работ и др.). Свойство, учитывающее как ремонтопригодность объекта, так и организационные факторы, определяют восстанавливаемость объектов (ОТС).

В общем случае, помимо ремонтопригодности в узком смысле, данное понятие включает в себя «обслуживаемость», то есть приспособленность объекта к техническому обслуживанию, «контролепригодность» и приспособленность к предупреждению и обнаружению отказов и повреждений, а также причин, их вызывающих. Более общее понятие «поддерживаемость», «эксплуатационная технологичность» включает в себя ряд технико-экономических и организационных факторов, например, качество подготовки обслуживающего персонала, в составе ОТС, как это показано в п.п. 1.4, 1.5.

Наиболее распространенными показателями ремонтопригодности являются:

· вероятность выполнения работ за заданное время (вероятность своевременного выполнения работ);

· среднее время выполнения работ;

· интенсивность восстановления.

Пусть 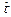фактическое, а 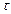допустимое время выполнения комплекса восстановительных работ, то первым показателем ремонтопригодности (восстанавливаемости) будет вероятность восстановления объекта за время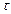

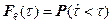, (5.1)

а вторым – среднее время восстановления (математическое ожидание времени восстановления)

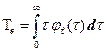, (5.2)

где 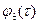- плотность вероятности восстановления.

Учитывая, что 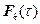есть не что иное, как функция распределения времени восстановления, то [2,5]

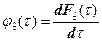, (5.3)

откуда

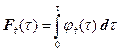. (5.4)

Функция (5.4) называется функцией восстановления, где 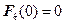и .

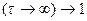Вывод аналитической зависимости для среднего времени восстановления, т.е. 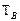аналогичен выводу (3.9) для среднего времени 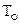безотказной работы.

Так, при известных функциях (5.1) и (5.3) можно записать

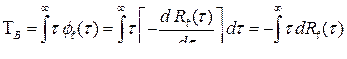. (5.5)

После интегрирования полученного выражения (5.5) по частям имеет место

;

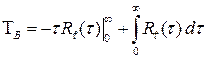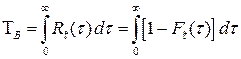. (5.6)

По аналогии с интенсивностью отказа (3.12) интенсивность 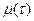восстановления есть вероятность того, что восстановление произойдет на бесконечно малом интервале времени 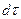, примыкающем к моменту времени 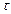при условии, что восстановление, начатое в момент времени 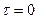, к моменту времени 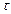еще не закончено.

Таким образом, безусловная вероятность восстановления на интервале 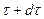запишется следующим образом

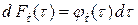. (5.7)

С другой стороны, это же событие (восстановление на интервале 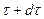) может быть представлено как одновременное выполнение двух условий (событий):

на интервале 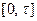восстановление не закончилось, вероятность этого условия равна ;

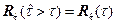восстановление на интервале 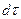, примыкающем к моменту времени 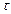, закончилось при условии, что к этому моменту времени 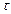оно еще не было завершено, вероятность этого события равна .

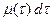Тогда на основании теоремы умножения вероятностей условная вероятность восстановления на интервале 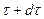составит

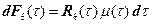. (5.8)

После подстановки 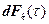из (5.4) формула (5.8) примет вид

,

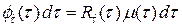откуда

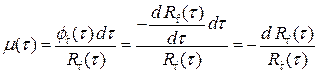. (5.9)

Интегрирование выражения (5.9) приводит к следующему результату

,

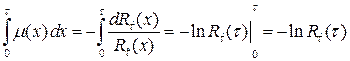откуда

,

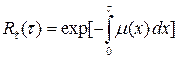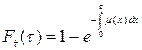. (5.10)

При 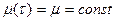выражения (5.10), (5.1), (5.3), (5.8), (5.10) преобразуются к виду

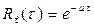; (5.11)

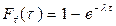; (5.12)

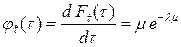; (5.13)

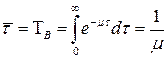. (5.14)

Таким образом, при экспоненциальном законе распределения времени 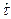восстановления интенсивность восстановления является постоянной величиной обратной среднему времени восстановления 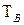, и характеризует «производительность» ОТС при устранении отказов объекта.

Связь между основными показателями восстанавливаемости (ремонтопригодности) (5.11) – (5.14) приведена на рис. 5.1

Для обеспечения требуемых значений показателей ремонтопригодности современные объекты выполняются по модульному принципу. С этой целью входящие в состав конструкции модули (отсеки, блоки, узлы и другие элементы) выполняются легкосъемными, а также предусматриваются различные люки, разъемы и встроенные элементы контроля, диагностирования и сигнализации.

Наряду с полученными выше показателями восстанавливаемости (ремонтопригодности) (5.11), (5.14) используется гамма-процентное время восстановления 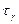- это время, в течение которого восстановление объекта будет осуществлено с вероятностью 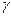, выраженной в процентах.

Так, при экспоненциальном законе распределения времени восстановления 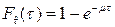гамма-процентное время восстановления, при котором объект восстанавливается с вероятностью 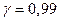определяется следующим образом

; ;

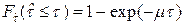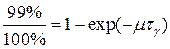откуда

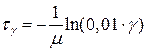. (5.15)