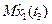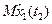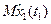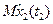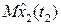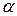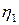Основные показатели долговечности.
Как известно, характер эксплуатации (функционирования) большинства объектов заключается в периодическом включении их в рабочее состояние. При этом каждое включение в рабочее состояние сопровождается определенным расходом технического ресурса (ресурса), под которым понимается наработка или объем работы объекта от начала эксплуатации или ее возобновления после среднего или капитального ремонта до наступления предельного состояния. Причем многообразие факторов приводит к тому, что интервал 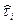 между моментами
между моментами 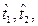 … включений объекта в рабочее состояние и продолжительность или объем работы объекта при каждом включении являются случайными величинами.
… включений объекта в рабочее состояние и продолжительность или объем работы объекта при каждом включении являются случайными величинами.
Это позволяет представить объект как систему, в которой каждая заявка, поступающая в случайные моменты времени  ,
, 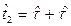 ,
,  , …, удовлетворяется комплексной наработкой в виде одного цикла «включения-отключения» и некоторого объема
, …, удовлетворяется комплексной наработкой в виде одного цикла «включения-отключения» и некоторого объема 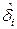 полезной работы, выполняемом при одном включении (см. п.2.2.). Тогда значения наработок в виде числа
полезной работы, выполняемом при одном включении (см. п.2.2.). Тогда значения наработок в виде числа 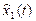 циклов «включений-отключений» и продолжительности (объема)
циклов «включений-отключений» и продолжительности (объема) 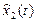 работы или нахождения объекта во включенном состоянии (нахождения под нагрузкой) к произвольному моменту времени t составит
работы или нахождения объекта во включенном состоянии (нахождения под нагрузкой) к произвольному моменту времени t составит
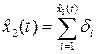 ,
, 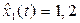 , …, (4.4)
, …, (4.4)
что соответствует модели постепенных отказов, обусловленных накоплением повреждений (см. п.2.2).
Причем число  циклов “включений-отключений” объекта на различных этапах его жизненного цикла может быть весьма велико. В этом случае независимо от вида законов распределения случайных величины
циклов “включений-отключений” объекта на различных этапах его жизненного цикла может быть весьма велико. В этом случае независимо от вида законов распределения случайных величины 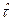 и δ наработки
и δ наработки  и
и 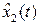 , образуют систему двух асимптотически нормальных величин или нормальный закон на плоскости. Его центры рассеивания М
, образуют систему двух асимптотически нормальных величин или нормальный закон на плоскости. Его центры рассеивания М  и М
и М 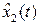 и дисперсии D
и дисперсии D  , D
, D 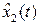 , выражаются через математические ожидания Т1, Т2 и дисперсии d1, d2 случайных величин
, выражаются через математические ожидания Т1, Т2 и дисперсии d1, d2 случайных величин 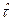 и δ в виде функций календарного времени t, а коэффициент корреляции
и δ в виде функций календарного времени t, а коэффициент корреляции 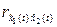 между наработками
между наработками  ,
, 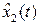 , также выражаясь через эти параметры, от времени не зависит, то есть [2,5,8]
, также выражаясь через эти параметры, от времени не зависит, то есть [2,5,8]
 М
М  ~
~ 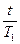 ; М
; М 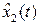 ~
~ 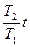 ;
;
D  ~
~ 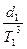 ;D
;D 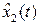 ~
~ 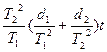 ; (4.5)
; (4.5)
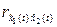 ~
~ 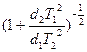 .
.
|
|
|
|
|
|
| |
| |
|
|
|
| |
|

|
| |
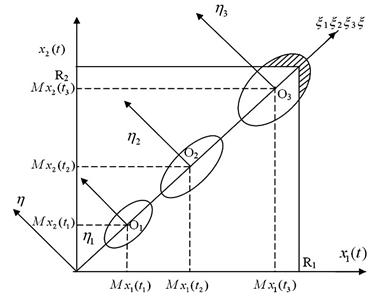
Рис 4.1. Эллипсы рассевания наработок в виде суммарного числа включений и суммарной наработки  .
.
Для большинства современных объектов обычно устанавливаются назначенные ресурсы в виде числа R1 циклов «включений-отключений» и времени R2 нахождения во включенном состоянии.
С учетом сказанного функция долговечности объекта P (t, R1, R2) может быть выражена через вероятность попадания случайной точки наработок с координатами  ,
, 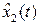 в пределе прямоугольной области назначенных ресурсов со сторонами R1 и R2 (рис. 4.1)
в пределе прямоугольной области назначенных ресурсов со сторонами R1 и R2 (рис. 4.1)
P (t; R1, R2) = 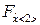 (R1, R2, t) = P {[
(R1, R2, t) = P {[  < R1][
< R1][ 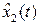 < R2]}, (4.6)
< R2]}, (4.6)
то есть через функцию распределения Fx<2> (R1, R2, t) двух случайных величин на плоскости (рис. 4.1)
После выбора новой координатной системы ξοη, центр которой совпадает с центром старой системы координат  , 0
, 0 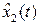 , а ось абсцисс совпадает с главной осью эллипса рассеивания наработок, и несложных преобразований, связанных с приведением нормального закона на плоскости к каноническому виду, функция долговечности (4.6) объекта может быть представлен в виде [2]
, а ось абсцисс совпадает с главной осью эллипса рассеивания наработок, и несложных преобразований, связанных с приведением нормального закона на плоскости к каноническому виду, функция долговечности (4.6) объекта может быть представлен в виде [2]
 P (t, R1, R2) = {
P (t, R1, R2) = { 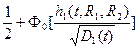 }{
}{ 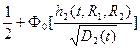 };
};
h1 (t, R1, R2) = [R1 - М 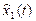 ] cos α + [R2 - М
] cos α + [R2 - М 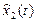 ] sin α;
] sin α;
h2 (t, R1, R2) = [R1 - М 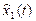 ] sin α + [R2 - М
] sin α + [R2 - М 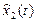 ] cos α; (4.7)
] cos α; (4.7)
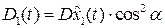 +
+ 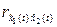 sin 2α
sin 2α 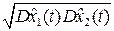 +
+ 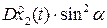 ;
;
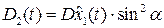 +
+ 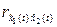 sin 2α
sin 2α 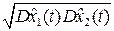 +
+ 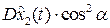 ;
;

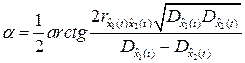 .
.
Угол a, составляемый осью рассеивания наработок с осью абсцисс 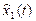 , лежит в первой четверти, если аргумент под знаком арктангенса положителен, то есть при D
, лежит в первой четверти, если аргумент под знаком арктангенса положителен, то есть при D  >D
>D 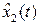 . В противном случае угол a отрицателен и лежит в четвертой четверти.
. В противном случае угол a отрицателен и лежит в четвертой четверти.
Замена в формулах (4.7) М  и М
и М 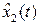 , D
, D  , D
, D 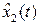 ,
, 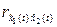 их асимптотическими значениями из формул (4.5) с последующей группировкой членов, содержащих t, R1, R2, позволяет выразить вероятность (4.6) с помощью трехпараметрических функций Лапласа (распределение Бернштейна) [2-5],
их асимптотическими значениями из формул (4.5) с последующей группировкой членов, содержащих t, R1, R2, позволяет выразить вероятность (4.6) с помощью трехпараметрических функций Лапласа (распределение Бернштейна) [2-5],
P (t, R1, R2) = { 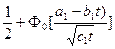 }{
}{ 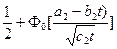 , (4.8)
, (4.8)
где


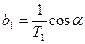 +
+ 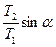 ;
;  -
-  ;
;
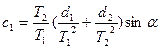 +
+ 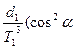 +
+ 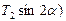 ; (4.9)
; (4.9)
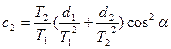 +
+ 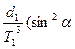 +
+ 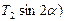 ;
;
α = 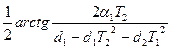 .
.
Вероятность (4.8) представляет собой дополнительную функцию распределения сроков службы объекта при заданных значениях R1, R2, ресурсов. И наоборот, при заданном сроке службы t вероятность (4.8) может рассматриваться как функция двух случайных аргументов 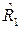 и
и 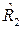 . В последнем случае, как нетрудно убедиться, она будет представлять собой функцию Fx<2> (R1, R2, t) двумерного нормального распределения случайных величин
. В последнем случае, как нетрудно убедиться, она будет представлять собой функцию Fx<2> (R1, R2, t) двумерного нормального распределения случайных величин 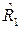 и
и 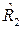 , приведенную к каноническому виду [2,5,8,9]. Действительно, из формул (4.6), (4.8) следует, что
, приведенную к каноническому виду [2,5,8,9]. Действительно, из формул (4.6), (4.8) следует, что
при R1 = 0, R2 = 0, P (R1, R2, t) = 0;
при R1 ® 0, R2 ® ¥, P (R1, R2, t) ® 1.
С учетом выражения (4.8) дополнительную функцию двумерного нормального распределения случайных величин 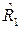 и
и 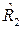 , обеспечивающих заданное значение t срока службы объекта, можно записать в следующем виде
, обеспечивающих заданное значение t срока службы объекта, можно записать в следующем виде
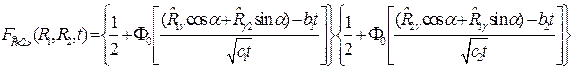 . (4.10)
. (4.10)
На основе полученных выражений (4.8), (4.9) условия (4.1), (4.2) для определения области (R1g, R2g) гамма-процентных ресурсов и гамма-процентного срока службы tg приобретают следующий вид:
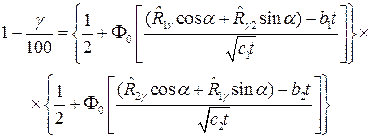 (4.11)
(4.11)
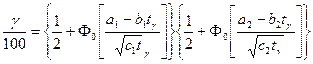 . (4.12)
. (4.12)
Дата добавления: 2016-09-26; просмотров: 1972;