Метод определения оптимальных сроков службы ОТС с учетом характера их применения
По мере увеличения количества и сложности ОТС и входящих в их состав элементов, а также роста предъявляемых к ним требований становится весьма актуальной проблема нахождения наиболее выгодных с точки зрения достижения поставленной цели решений о сроках службы. Однако значительное рассеивание фактических сроков службы даже номинально одинаковых объектов при идентичных условиях эксплуатации приводит к необходимости статистического подхода к оценке приемлемых сроков службы, удовлетворяющих условиям реализации поставленной цели. Под целью обычно понимается определенный, заранее запланированный результат, который должен быть достигнут с помощью определенных действий и средств. Так, при оценке оптимального срока службы 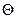 совокупности однотипных объектов
совокупности однотипных объектов 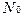 , которые должны выполнить заданный объем работ в любой момент
, которые должны выполнить заданный объем работ в любой момент 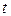 поступления заявки на их использование, почти всегда приходится руководствоваться необходимостью так определить величину
поступления заявки на их использование, почти всегда приходится руководствоваться необходимостью так определить величину 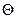 , чтобы:
, чтобы:
– иметь максимально возможное количество работоспособных объектов из числа введенных в строй к этому моменту;
– обеспечить как можно более длительный интервал их эксплуатации 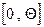 .
.
Суммируя эти требования, можно сказать, что необходимо иметь как можно большее количество исправных объектов в течение возможно более длительного промежутка времени. Эти требования по своей природе противоречивы, ибо с течением времени число отказавших объектов будет увеличиваться, а доля исправно работающих (даже при наличии восстановления) – уменьшается. Под отказом в данном случае понимается достижение элементом (объектом) ОТС одного из предельных состояний, определяющих невозможность его дальнейшей эксплуатации. Такое применение понятия «отказ» при решении ряда задач, связанных со сроком службы, позволяет использовать хорошо разработанный математический аппарат теории надежности.
Таким образом, при поступлении заявки на использование в любой момент времени 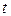 , когда восстановление отсутствует, заданный объем работы будет выполнен лишь частью объектов
, когда восстановление отсутствует, заданный объем работы будет выполнен лишь частью объектов 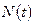 , исправных к этому моменту времени. Следовательно, способность рассматриваемой совокупности объектов удовлетворять перечисленным выше требованиям (поставленной цели) в любой момент времени
, исправных к этому моменту времени. Следовательно, способность рассматриваемой совокупности объектов удовлетворять перечисленным выше требованиям (поставленной цели) в любой момент времени 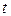 будет характеризоваться функцией
будет характеризоваться функцией
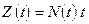 . (4.28)
. (4.28)
Функция 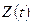 представляет собой суммарный срок службы объектов, готовых к применению в любой момент
представляет собой суммарный срок службы объектов, готовых к применению в любой момент 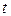 , и определяет способность рассматриваемой совокупности объектов удовлетворять сформулированным выше требованиям с течением времени, т.е. характеризует собой суммарный эффективный срок службы. Разделив обе части выражения (4.28) на количество объектов
, и определяет способность рассматриваемой совокупности объектов удовлетворять сформулированным выше требованиям с течением времени, т.е. характеризует собой суммарный эффективный срок службы. Разделив обе части выражения (4.28) на количество объектов 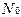 , введенных в эксплуатацию к моменту
, введенных в эксплуатацию к моменту 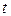 , получим
, получим
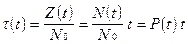 , (4.29)
, (4.29)
где 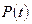 – функция надежности или долговечности рассматриваемой совокупности объектов. Функция
– функция надежности или долговечности рассматриваемой совокупности объектов. Функция 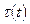 определяет, какую часть от текущего календарного времени
определяет, какую часть от текущего календарного времени 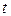 составляет средний эффективный срок службы конкретного объекта. Действительно, при
составляет средний эффективный срок службы конкретного объекта. Действительно, при 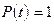
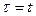 , а при
, а при 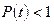
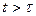 . Выражение (4.29) характеризует риск потребителя (пользователя) при принятии решения о сроке службы.
. Выражение (4.29) характеризует риск потребителя (пользователя) при принятии решения о сроке службы.
Естественно, что оптимальный срок службы 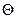 рассматриваемой совокупности объектов или ОТС в целом должен определяться, исходя из максимального соответствия поставленной цели, определяемой формулами (4.28), (4.29), запланированному результату, т.е. из всех возможных значений
рассматриваемой совокупности объектов или ОТС в целом должен определяться, исходя из максимального соответствия поставленной цели, определяемой формулами (4.28), (4.29), запланированному результату, т.е. из всех возможных значений 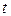 должно быть выбрано
должно быть выбрано 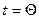 , доставляющее максимум выражению (4.29). Отсюда
, доставляющее максимум выражению (4.29). Отсюда
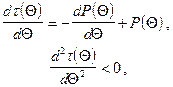 (4.30)
(4.30)
где 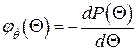 – функция плотности распределения отказов (предельных состояний). Тогда из выражения (4.30) следует
– функция плотности распределения отказов (предельных состояний). Тогда из выражения (4.30) следует
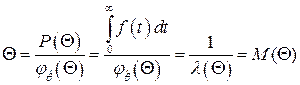 , (4.31)
, (4.31)
где 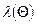 – интенсивность отказов-замен объектов;
– интенсивность отказов-замен объектов;
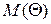 - отношение Милса
- отношение Милса
Решение уравнения (4.31) сводится к отысканию на числовой оси такого значения 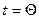 , при котором соответствующие ему значения
, при котором соответствующие ему значения 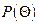 и
и 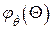 при делении первого на второе дают частное, равное
при делении первого на второе дают частное, равное 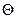 . При
. При 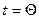 происходит полная компенсация уменьшения суммарного эффективного срока службы исправных объектов вследствие отказов за счет увеличения срока службы исправных. При
происходит полная компенсация уменьшения суммарного эффективного срока службы исправных объектов вследствие отказов за счет увеличения срока службы исправных. При 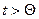 наступление отказов (предельных состояний) принимает массовый характер и их влияние становится решающим. У реальных объектов или ОТС может совмещаться несколько типов отказов в соответствии с их предельными состояниями. При предположении, что отказы возникают независимо друг от друга выражение (4.29) принимает вид
наступление отказов (предельных состояний) принимает массовый характер и их влияние становится решающим. У реальных объектов или ОТС может совмещаться несколько типов отказов в соответствии с их предельными состояниями. При предположении, что отказы возникают независимо друг от друга выражение (4.29) принимает вид
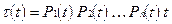 ,
,
откуда
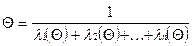 , (4.32)
, (4.32)
где 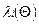 – функция интенсивности отказов или замен (
– функция интенсивности отказов или замен ( 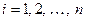 ).
).
Ряд значений 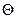 , вычисленных по формулам (4.31), (4.32) для различных законов распределения отказов, приведен в табл. 4.2.
, вычисленных по формулам (4.31), (4.32) для различных законов распределения отказов, приведен в табл. 4.2.
Таблица 4.2. Оптимальные значения сроков службы при различных законах их распределения
| Типы распределений отказов | Плотность распределения | Функция надежности | Оптимальный срок службы θ |
| Экспонен-циальное | 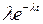
| 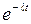
| 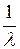
|
| Равномерное | 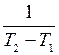
| 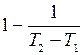
| 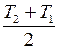
|
| Вейбулла | 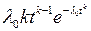
| 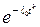
| 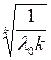
|
| Релея | 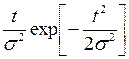
| 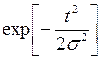
| 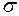
|
| Степенное | 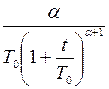
| 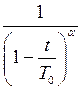
| 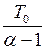
|
| Нормальное | 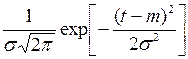
| 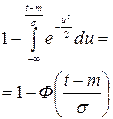
| 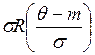
|
| Два нормальных | 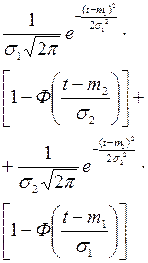
| 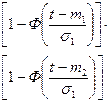
| 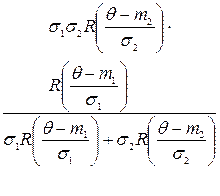
|
| Вейбулла и экспонен-циальное | 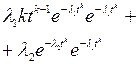
| 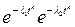
| 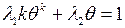
|
Особый интерес представляет случай, когда отказы распределены по нормальному закону. Тогда из выражения (4.31) следует, что
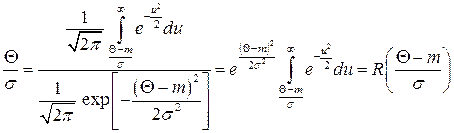 . (4.33)
. (4.33)
где функция 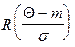 , представляющая собой отношение «хвоста» распределения к плотности распределения, называемое отношением Миллса [2,18]. Отсюда при
, представляющая собой отношение «хвоста» распределения к плотности распределения, называемое отношением Миллса [2,18]. Отсюда при 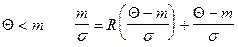 . Значения функции
. Значения функции 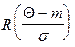 могут быть затабулированы, что позволит легко определить величину
могут быть затабулированы, что позволит легко определить величину 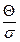 при известных параметрах нормального распределения
при известных параметрах нормального распределения 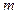 и
и 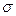 по табл. 4.3.
по табл. 4.3.
Таблица 4.3.
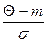
| 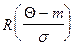
| 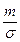
| 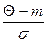
| 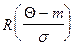
| 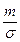
| 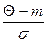
| 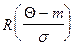
| 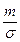
|
| -3.0 | 227.0 | 300.0 | -2.0 | 18.1 | 20.1 | -1.0 | 3.5 | 4.5 |
| -2.9 | 166.3 | 169.2 | -1.9 | 14.8 | 16.7 | -0.9 | 3.1 | 4.0 |
| -2.7 | 95.8 | 98.5 | -1.7 | 10.2 | 11.9 | -0.7 | 2.4 | 3.1 |
| -2.6 | 73.2 | 75.8 | -1.6 | 8.5 | 10.1 | -0.6 | 2.2 | 2.8 |
| -2.5 | 56.8 | 59.3 | -1.5 | 7.2 | 8.7 | -0.5 | 2.0 | 2.5 |
| -2.4 | 44.3 | 46.7 | -1.4 | 6.1 | 7.5 | -0.4 | 1.8 | 2.2 |
| -2.3 | 35.0 | 37.3 | -1.3 | 5.3 | 6.6 | -0.3 | 1.6 | 1.9 |
| -2.2 | 27.8 | 30.0 | -1.2 | 4.6 | 5.8 | -0.2 | 1.5 | 1.7 |
| -2.1 | 22.3 | 24.4 | -1.1 | 4.0 | 5.1 | -0.1 | 1.4 | 1.5 |
Так, например, при 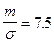 значение
значение 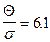 .
.
Следует отметить, что в большинстве случаев величина 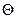 по формулам (4.31), (4.32), (4.33) в конечном виде не вычисляется и возможно лишь приближенное решение.
по формулам (4.31), (4.32), (4.33) в конечном виде не вычисляется и возможно лишь приближенное решение.
Таким образом, изложенный выше подход к оценке оптимального срока службы 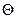 позволяет при известных типах распределения отказов (предельных состояний) так выбрать его, чтобы суммарная продолжительность сроков службы объектов, работоспособных к моменту
позволяет при известных типах распределения отказов (предельных состояний) так выбрать его, чтобы суммарная продолжительность сроков службы объектов, работоспособных к моменту 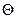 , была максимальной, т.е. полностью использовать способность объектов или ОТС рассматриваемой совокупности удовлетворять поставленной цели: иметь возможно большее количество исправных объектов в течение возможно более длительного промежутка времени, содержащего возможный момент поступления заявки на их применение. Для практического определения величины
, была максимальной, т.е. полностью использовать способность объектов или ОТС рассматриваемой совокупности удовлетворять поставленной цели: иметь возможно большее количество исправных объектов в течение возможно более длительного промежутка времени, содержащего возможный момент поступления заявки на их применение. Для практического определения величины 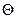 по формулам (4.31), (4.32), (4.33) необходимо знание лишь начальной части кривой плотности распределения отказов, что значительно облегчает задачу в случае, когда данные о типах распределения отказов отсутствуют. Величина
по формулам (4.31), (4.32), (4.33) необходимо знание лишь начальной части кривой плотности распределения отказов, что значительно облегчает задачу в случае, когда данные о типах распределения отказов отсутствуют. Величина 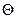 и соответствующее ей значение функции надежности
и соответствующее ей значение функции надежности 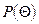 однозначно определяют оптимальный гамма-процентный ресурс объектов в зависимости от их внутренних свойств и особенностей применения. Значение
однозначно определяют оптимальный гамма-процентный ресурс объектов в зависимости от их внутренних свойств и особенностей применения. Значение 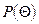 при этом устанавливает минимально допустимый в соответствии со сформулированными условиями оптимальности уровень безотказности и может быть использовано при задании минимально допустимого уровня безотказности (долговечности) объекта или ОТС в целом на этапе проектирования при известных расчетных данных о надежности его элементов.
при этом устанавливает минимально допустимый в соответствии со сформулированными условиями оптимальности уровень безотказности и может быть использовано при задании минимально допустимого уровня безотказности (долговечности) объекта или ОТС в целом на этапе проектирования при известных расчетных данных о надежности его элементов.
4.7 Оценка сроков службы объектов с учетом физического
и морального износа
Ряд технико-экономических задач сводится к задаче о замене объектов, прекращения и возобновления процессов и т.д., т.е. к установлению наиболее оптимальных сроков службы объектов (ОТС) и времени производственных процессов. Наиболее общим и приемлемым критерием замены объекта, возобновления процесса эксплуатации следует, по-видимому, считать получение определенного выигрыша или «прибыли» в результате замены по сравнению с продолжающим работать старым объектов [4]. Так как в реальных условиях характеристики ОТС или объектов в ее составе или процессов функционирования меняются, то под выигрышем 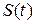 может пониматься сумма накапливающихся со временем мгновенных значений разностей между выходными параметрами нового объекта, работающего с момента замены
может пониматься сумма накапливающихся со временем мгновенных значений разностей между выходными параметрами нового объекта, работающего с момента замены 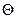 , и старого объекта при условии, если бы последний продолжал работать без замены. На рис. 4.3 выигрыш или «прибыль» представлены заштрихованной областью
, и старого объекта при условии, если бы последний продолжал работать без замены. На рис. 4.3 выигрыш или «прибыль» представлены заштрихованной областью 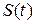 , где
, где 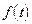 – характеристика затрат на эксплуатацию заменяемого объекта;
– характеристика затрат на эксплуатацию заменяемого объекта; 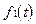 – характеристика затрат на эксплуатацию нового
– характеристика затрат на эксплуатацию нового  объекта;
объекта; 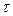 – произвольно выбранный момент времени.
– произвольно выбранный момент времени.
|
|
|
| |
|
| |
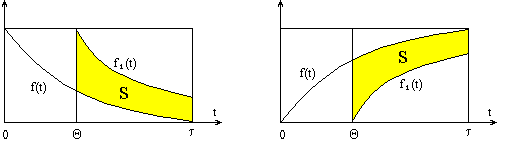
Рис. 4.3. Характеристики процесса эксплуатации заменяемого и нового объектов
Так, на рис. 4.3.а приведены характеристики надежности объектов, а на рис. 4.3.б стоимость эксплуатационных затрат.
Тогда выигрыш, получаемый в результате замены оборудования, будут определяться следующим образом:
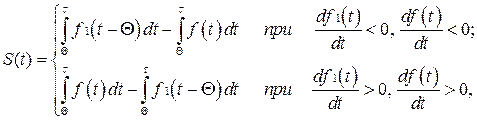 (4.34)
(4.34)
где 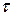 - планируемый интервал замены
- планируемый интервал замены 
Продифференцировав выражение (4.34) по 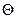 и приравняв полученный результат нулю, получим формулу для определения оптимального времени замены объекта на интервале
и приравняв полученный результат нулю, получим формулу для определения оптимального времени замены объекта на интервале 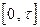 дающего максимальный выигрыш:
дающего максимальный выигрыш:
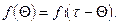 (4.35)
(4.35)
Формула (4.35) учитывает влияние морального износа на оптимальный срок замены, поскольку 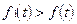 [16-18]. Частным случаем является замена объекта эквивалентным
[16-18]. Частным случаем является замена объекта эквивалентным 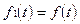 . Тогда из (4.35) следует
. Тогда из (4.35) следует 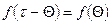 , откуда
, откуда
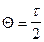 . (4.36)
. (4.36)
Таким образом, при любом значении 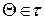 оптимальное время замены объекта будет определяться выражениями (4.35) и (4.36), где
оптимальное время замены объекта будет определяться выражениями (4.35) и (4.36), где 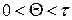 . Подстановка этого значения в выражение (4.34), после интегрирования дает значение оптимального выигрыша
. Подстановка этого значения в выражение (4.34), после интегрирования дает значение оптимального выигрыша 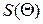 .
.
Полученные результаты (4.34) – (4.36) позволяют моральный износ первого и второго рода [5,18].
Пример. Пусть начальная годовая прибыль в единицу времени, находящегося в эксплуатации объекта С,а такая же прибыль созданных и находящихся на рынке к моменту замены объектов составляет С1. Прибыль в процессе эксплуатации этих объектов снижается по экспоненциальным законам и соответственно составляет
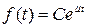 и
и 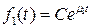 , (4.37)
, (4.37)
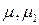 - показатели роста эксплуатационных затрат соответственно старого и нового объектов.
- показатели роста эксплуатационных затрат соответственно старого и нового объектов.
Тогда в соответствии с формулой (4.25) оптимальное время 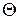 замены, находящегося в эксплуатации объекта новым с учетом выражения (4.37) запишется следующим образом
замены, находящегося в эксплуатации объекта новым с учетом выражения (4.37) запишется следующим образом
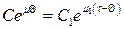 ,
,
откуда 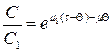 ;
; 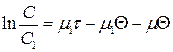 ,
,
и окончательно
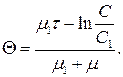 (4.38)
(4.38)
Полученное выражение (4.38) позволяет учесть моральный износ первого и второго рода.
1. При 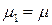 и
и 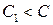 , имеет место моральный износ первого рода, когда на рынке появились объекты, аналогичные по свойствам старому объекту, но более дешевые. Тогда формула (4.38) приобретает вид
, имеет место моральный износ первого рода, когда на рынке появились объекты, аналогичные по свойствам старому объекту, но более дешевые. Тогда формула (4.38) приобретает вид
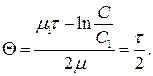 (4.29)
(4.29)
В этом случае, когда на интервале замены 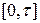 объект заменяется аналогичным, то из формул (4.38) и (4.39) следует
объект заменяется аналогичным, то из формул (4.38) и (4.39) следует 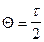 , что полностью совпадает с ранее полученной формулой (4.36).
, что полностью совпадает с ранее полученной формулой (4.36).
2. При 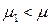 и
и 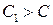 имеет место износ второго рода, когда на рынке появились более совершенные по эксплуатационным свойствам объекты
имеет место износ второго рода, когда на рынке появились более совершенные по эксплуатационным свойствам объекты 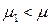 , но более дорогие объекты
, но более дорогие объекты 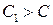 . В этом случае срок замены объекта на интервале
. В этом случае срок замены объекта на интервале 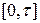 будет определяться формулой (4.38).
будет определяться формулой (4.38).
Рассмотренный подход позволяет производить оценку сроков службы ОТС и ее элементов из условий экономической целесообразности их использования на предполагаемом интервале 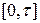 .
.
Дата добавления: 2016-09-26; просмотров: 2628;











