Модель отказов при мгновенных повреждениях.
Эти отказы наступают в случаях, когда нагрузка 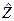 , имеющая случайный характер, превысит сопротивляемость, прочность или несущую способность
, имеющая случайный характер, превысит сопротивляемость, прочность или несущую способность 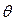 объекта. При этом предполагается, что вариации нагрузки образуют однородную по времени случайную последовательность, другими словами имеет место стационарный режим нагружения, где ^ - символ случайной величины.
объекта. При этом предполагается, что вариации нагрузки образуют однородную по времени случайную последовательность, другими словами имеет место стационарный режим нагружения, где ^ - символ случайной величины.
Если действующее значение нагрузки 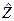 превзойдёт прочность (несущую способность), то немедленно произойдёт отказ, критерием которого является предикат вида
превзойдёт прочность (несущую способность), то немедленно произойдёт отказ, критерием которого является предикат вида
( 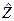 >
> 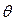 ). (2.1)
). (2.1)
Если же действующее значение нагрузки 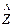 в ходе единичного цикла нагружения не превысит прочность (несущую способность), то отказ не возникнет, то есть
в ходе единичного цикла нагружения не превысит прочность (несущую способность), то отказ не возникнет, то есть
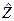 ≤
≤ 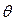 . (2.2)
. (2.2)
Предикаты (2.1),(2.2) соответственно являются критериям и отказа и безотказной работы объекта.
При формировании критериев (2.1), (2.2) исходят из следующих двух положений:
1.Уровень предельно допустимой нагрузки (несущей способности) 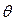 в вероятностном смысле остаётся постоянным в течение всего времени эксплуатации объекта.
в вероятностном смысле остаётся постоянным в течение всего времени эксплуатации объекта.
2.Отказ возникает не как следствие постепенного изменения внутреннего состояния объекта, а лишь как следствие внешнего случайного воздействия.
Поскольку в этих условиях отказ возникает лишь по причине внешнего воздействия на объект, то замена старого объекта на новый не может повлиять на причину отказа. Не может повлиять на неё и ремонт, поэтому единственный путь повышения надежности состоит либо в конструктивном улучшении объекта, либо в снижении действующих на него нагрузок.
Таким образом, на основе критерия (2.2) вероятность безотказной работы объекта при единичном цикле нагружения составит
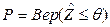 , (2.3)
, (2.3)
а вероятность отказа в соответствии с критерием (2.1) составит
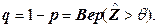 (2.4)
(2.4)
Процесс эксплуатации объекта в общем случае представляет собой случайную последовательность циклов его нагружений. Тогда, вероятность того, что объект откажет в k- ом цикле нагружения с учётом формул (2.3), (2.4) запишется следующим образом
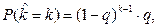 (2.5)
(2.5)
где 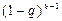 - вероятность того, что объект не откажет в предшествующих
- вероятность того, что объект не откажет в предшествующих 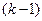 циклах нагружения.
циклах нагружения.
Здесь под циклом нагружения понимается такое нагружение, при котором объект, выполняя предписанные ему функции, подвергается воздействию всего спектра действующих на него перегрузок.
Отсюда следует, что вероятность того, что за первые к циклов нагружения отказ произойдет, то есть вероятность события 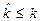 запишется в виде [2-5]
запишется в виде [2-5]
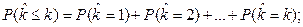 k=1, 2,…, (2.6)
k=1, 2,…, (2.6)
откуда
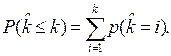 (2.7)
(2.7)
С учётом (2.5) формула (2.7) примет вид [6.8]
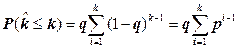 . (2.8)
. (2.8)
Сумма в правой части выражения (2.8) представляет собой сумму k членов геометрической прогрессии [2-5],
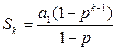 ,
,
на основе которой при 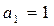 и с учётом (2.4) формула (2.8) преобразуется к виду
и с учётом (2.4) формула (2.8) преобразуется к виду
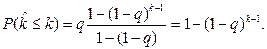 (2.9)
(2.9)
Полученное выражение (2.9) представляет собой вероятность отказа объекта за k циклов нагружения.
Тогда с учётом (2.9) вероятность безотказной работы объекта за k циклов нагружения примет вид
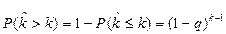 . (2.10)
. (2.10)
На основе выражения (2.10) может быть получено выражение для математического ожидания длительности безотказной работы объекта, выраженное в количестве k циклов нагружения и выражаемое суммой членов следующего ряда [2-5]:
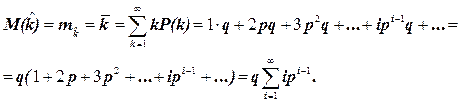 (2.11)
(2.11)
Ряд, стоящий в скобках правой части полученного выражения (2.11), представляет собой результат дифференцирования сходящейся геометрической прогрессии вида [2-5]:
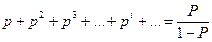 ,
,
дифференцирование обеих частей, которой приводит к следующему результату
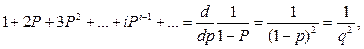 (2.12)
(2.12)
откуда с учётом (2.11) и (2.12)
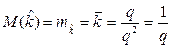 . (2.13)
. (2.13)
Дисперсия 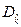 случайной величины
случайной величины 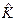 выражается через второй центральный момент
выражается через второй центральный момент 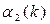 и математическое ожидание (2.13) случайной величины
и математическое ожидание (2.13) случайной величины 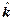 по формуле [2-5,18,19]
по формуле [2-5,18,19]
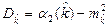 . (2.14)
. (2.14)
Выражение для второго центрального момента 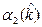 случайной величины
случайной величины 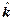 с учётом (2.11) выражается следующим образом [4,8]:
с учётом (2.11) выражается следующим образом [4,8]:
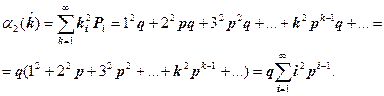 (2.15)
(2.15)
Для вычисления суммы сходящегося ряда необходимо выражение, стоящее в скобках в левой части формулы (2.15) умножить на p, тогда по аналогии с (2.12)
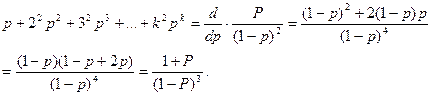 (2.16)
(2.16)
Формула (2.14) для дисперсии случайной величины 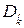 после умножения (2.16) на
после умножения (2.16) на 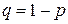 и с учетом (2.13) примет следующий вид:
и с учетом (2.13) примет следующий вид:
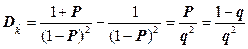 . (2.17)
. (2.17)
Поскольку значение q достаточно мало, то формула (2.17) может быть представлена следующим образом:
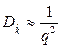 . (2.18)
. (2.18)
С другой стороны, после разложения в биномиальный ряд формула (2.9), учитывая, что значение k может быть достаточно велико, а значение q мало, может быть представлена следующим образом [2-5]:
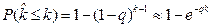 . (2.19).
. (2.19).
Поскольку из формулы (2.13) следует, что 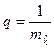 , то выражения (2.19), (2.10), (2.18) соответственно примут вид
, то выражения (2.19), (2.10), (2.18) соответственно примут вид
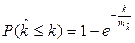 , (2.20)
, (2.20)
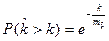 , (2.21)
, (2.21)
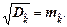 (2.22)
(2.22)
Во всех полученных выше формулах случайная величина 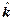 есть не что иное, как дискретное время. Однако в реальных условиях при решении большинства задач время выступает как величина непрерывная, когда интервал
есть не что иное, как дискретное время. Однако в реальных условиях при решении большинства задач время выступает как величина непрерывная, когда интервал 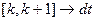 . В этом случае формулы (2.20), (2.21), (2.22) могут быть записаны следующим образом
. В этом случае формулы (2.20), (2.21), (2.22) могут быть записаны следующим образом
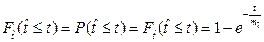 , (2.23)
, (2.23)
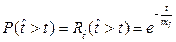 , (2.24)
, (2.24)
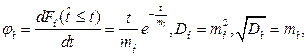 (2.25)
(2.25)
где 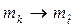 , то есть математическое ожидание времени безотказной работы объекта выражаемое не дискретной случайной величиной
, то есть математическое ожидание времени безотказной работы объекта выражаемое не дискретной случайной величиной 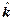 , а соответствующей ей непрерывной случайной величиной
, а соответствующей ей непрерывной случайной величиной 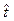 .
.
На рис. 2.1 приведены для сравнения графики функций 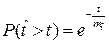 и
и 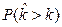
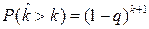 вычисленные по формулам (2.10), (2.24) с одинаковыми параметрами
вычисленные по формулам (2.10), (2.24) с одинаковыми параметрами 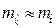 . Откуда следует хорошая сходимость дискретной и непрерывной моделей (2.20)-(2.22) и (2.23)-(2.25).
. Откуда следует хорошая сходимость дискретной и непрерывной моделей (2.20)-(2.22) и (2.23)-(2.25).
| |
|
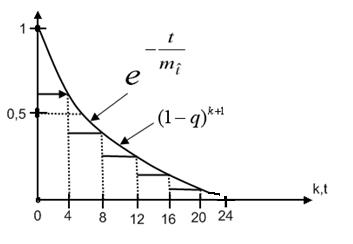
Рис.2.1 Графики вероятности безотказной работы для геометрического (2.9) и экспоненциального (2.23) распределений при 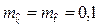 .
.
Дата добавления: 2016-09-26; просмотров: 1870;











