Дисперсионный анализ данных однофакторного полевого опыта
Цель дисперсионного анализа урожайных данных полевого опыта – установить существенность различий между урожаями отдельных вариантов, т.е. достоверность различий между выборочными средними арифметическими. В настоящее время он считается наиболее совершенным методом математической обработки данных полевых опытов. При дисперсионном анализе существенность влияния вариантов на урожай оценивается с помощью критерия F (Фишера), который представляет собой отношение дисперсии вариантов к остаточной:
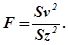
Ход дисперсионного анализа зависит от структуры опыта. Существует несколько моделей дисперсионного анализа, например: дисперсионный анализ однофакторных полевых опытов с однолетними культурами, дисперсионный анализ однофакторных полевых опытов с многолетними культурами, дисперсионный анализ многофакторных опытов, заложенных стандартными методами, методами расщепленных делянок, латинского квадрата и латинского прямоугольника.
Задание. Произвести обработку урожайных данных однофакторного полевого опыта методом дисперсионного анализа с применением произвольного начала (метод кодирования) при вычислении сумм квадратов отклонений.
Поделяночные урожаи в опыте изменяются от делянки к делянке (варьируют). Эта изменчивость вызывается различными причинами: во-первых, действием изучаемых в опыте вариантов; во-вторых, влиянием повторений – главным образом неодинаковым почвенным плодородием повторений и, в-третьих, влиянием случайных причин. Общее варьирование урожаев в опыте Су обусловлено совместным действием этих факторов изменчивости и равно поэтому сумме частных варьирований:
Су = Ср + Cv + Cz
где Ср – варьирование повторений, или систематические ошибки;
Cv – варьирование вариантов;
Сz – остаточное варьирование (случайные ошибки).
Таблица урожаев
| Вариант | Урожай по повторениям X, ц/га | Суммы по вариантам ΣV | Средние
по вариантам
 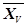
| |||
| I | II | III | IV | |||
| 16,5 | 17,2 | 16,2 | 14,3 | 64,2 | 16,0 | |
| 21,1 | 21,6 | 24,7 | 22,9 | 90,3 | 22,6 | |
| 14,7 | 14,6 | 12,8 | 13,9 | 56,0 | 14,0 | |
| 12,1 | 13,7 | 11,4 | 10,9 | 48,1 | 12,0 | |
| Сумма по повторениям ΣΡ | 64,4 | 67,1 | 65,1 | 62,0 | ΣX = 258,6 | 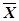 = 16,2 = 16,2
|
Средние по повторениям 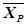
| 16,1 | 16,8 | 16,3 | 15,5 | - | - |
Общее и частного варьирования характеризуются соответствующими суммами квадратов отклонений урожаев в опыте. Вычисление сумм квадратов отклонений производится по-разному в зависимости от характера цифрового материлa и наличия вычислительной техники.
Если поделяночные урожаи выражаются небольшими числами, а средний урожай в опыте – целое число, то вычисление сумм квадратов отклонений можно вести прямым способом; при наличии счетных машин и таблиц квадратов чисел – с помощью корректирующего фактора. Но чаще всего применяется метод произвольного начала, особенно когда поделяночные урожаи выражаются многозначными, громоздкими цифрами.
В качестве произвольного начала выбирают целое запоминающееся число, близкое к среднему урожаю в опыте (в нашем примере – 15 ц/га). Для облегчения расчетов составляют вспомогательную таблицу.
Вспомогательная таблица состоит из двух половин – левой и правой. В левой записывают отклонения урожаев в опыте от произвольного начала, а в правой – их квадраты.
Таблица отклонений и квадратов отклонений
от произвольного начала А = 15 ц/га
| Вариант | Отклонения Х1 | V | Квадраты отклонений 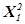
| V2 | ||||||
| I | II | II | IV | I | II | II | IV | |||
| +1,5 | +2,2 | +1,2 | -0,7 | +4,2 | 2,25 | 4,84 | 1,44 | 0,49 | 17,64 | |
| +6,1 | +6,6 | +9,7 | +7,9 | +30,3 | 37,21 | 43,56 | 94,09 | 62,41 | 918,09 | |
| -0,3 | -0,4 | -2,2 | -1,1 | -4,0 | 0,09 | 0,16 | 4,84 | 1,21 | 16,00 | |
| -2,9 | -1,3 | -3,6 | -4,1 | -11,9 | 8,41 | 1,69 | 12,96 | 16,81 | 141,61 | |
| Р | +4,4 | +7,1 | +5,1 | +2,0 | ΣХ1 = +18,6 | 19,36 | 50,41 | 26,01 | 4,00 | (ΣХ1)2 = 345,96 |
В средней части левой половины таблицы проставляют со знаком плюс или минус отклонения поделяночных урожаев от произвольного начала (X–А) или сокращенно X1 : 16,5 – 15,0 = + 1,5; 21,1 – 15,0 = +6,1 ... 10,9 – 15,0 = –4,1. В нижней горизонтальной строке Р показывают суммарные отклонения по каждому повторению опыта. Например, по первому повторению: (+1,5) + (6,1) + (–0,3) + (–2,9) = +4,4. В столбце V – суммарные отклонения по каждому варианту. Например, по первому: (+1,5) + (+ 2,2) + (+ 1,2) + (–0,7) = +4,2. На стыке строки Р и столбца V в нижнем правом углу левой половины таблицы записывается сумма всех поделяночных отклонений ΣX1. Она может быть получена двояким путем: как алгебраическая сумма суммарных отклонений по повторениям и то же самое по вариантам опыта, т. е. ΣХ1 = ΣР = ΣV. В нашем примере ΣХ1 = (+ 4,4) + (+ 7,1) + (+ 5,1) + (+ 2,0) = (+ 4,2) + (+ 30,3) + (–4,0) + (–11,9) = +18,6.
После заполнения левой половины таблицы проверяют правильность вычисления отклонений по равенству ΣX = AN + ΣX1 · ΣX берут из таблицы урожаев, N (число делянок в опыте) = ln. В нашем примере ΣX = 258,6 = 15 · 16 + (+18,6).
В центре правой половины таблицы проставляют квадраты отклонений поделяночных урожаев от произвольного начала 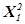 : 1,52 = 2,25; 6,12 = 37,21; ... (–4,1)2 = 16,81; под ними – квадраты суммарных отклонений по повторениям Р2: 4,42 = 19,36; 7,12 = 50,41; 5,12 = 26,01; 2,02 = 4,0; в столбце V2 – квадраты сумм отклонений по вариантам опыта: (+ 4,2)2 = 17,64; ( + 30,3)2 = 918,09; (–4,0)2 = 16,0; (–11,9)2 = 141,61. В нижнем правом углу записывают квадрат суммы поделяночных отклонений (ΣX1)2 = (+18,6)2 = 345,96.
: 1,52 = 2,25; 6,12 = 37,21; ... (–4,1)2 = 16,81; под ними – квадраты суммарных отклонений по повторениям Р2: 4,42 = 19,36; 7,12 = 50,41; 5,12 = 26,01; 2,02 = 4,0; в столбце V2 – квадраты сумм отклонений по вариантам опыта: (+ 4,2)2 = 17,64; ( + 30,3)2 = 918,09; (–4,0)2 = 16,0; (–11,9)2 = 141,61. В нижнем правом углу записывают квадрат суммы поделяночных отклонений (ΣX1)2 = (+18,6)2 = 345,96.
Ход дисперсионного анализа независимо от способов вычисления сумм квадратов отклонений следующий.
1. Определение общего варьирования(общей суммы квадратов). При использовании произвольного начала оно вычисляется по следующей рабочей формуле:
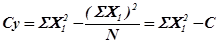 ,
,
где 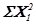 – сумма квадратов отклонений поделяночных урожаев от произвольного начала;
– сумма квадратов отклонений поделяночных урожаев от произвольного начала;
(EX1)2 – квадрат этой суммы;
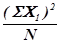 – корректирующий фактор С.
– корректирующий фактор С.
В нашем примере Су = 2,25 + 37,21 + ... +16,81 – 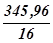 = 292,46 – 21,62 = 270,84.
= 292,46 – 21,62 = 270,84.
2. Определение варьирования повторений(суммы квадратов дляповторений).
Ср = ΣΡ2 : l – С,
где Р2 – сумма квадратов суммарных отклонений поделяночных урожаев по повторениям от произвольного начала;
l – число вариантов в опыте;
Ср = (19,36 + 50,41 + 26,01 + 4,0) : 4 – 21,62 = 24,95 – 21,62 = 3,33.
3. Определение варьирования вариантов(суммы квадратов для вариантов).
Cv = ΣV2 : n – C,
где ΣV2 – сумма квадратов суммарных отклонений поделяночных урожаев по вариантам от произвольного начала;
n – повторность опыта.
Cv= (17,64+ 918,09 + 16,0 + 141,61) : 4 – 21,62= 273,34 – 21,62 = 251,72.
4. Определение остаточного варьирования (остаточной суммы квадратов), т.е. той доли в колебаниях урожаев, которая появилась под влиянием случайных причин. Проще всего его определять как остаток по разности между общим варьированием и варьированием повторений и вариантов:
Сz = Су – Ср –Cv = 270,84 – 3,33 – 251,72 =15,79.
Внимание! Остаточная сумма квадратов может быть только положительным числом. Если она получалась отрицательной, следует проверить все предыдущие вычисления.
5. Вычисление дисперсий вариантов и остаточной. Для этого составляют таблицу дисперсионного анализа.
Таблица дисперсионного анализа
| Вид варьирования | Сумма квадратов отклонений | Число степеней свободы | Средний квадрат (дисперсия) | F | |
| фактич. | |||||
| Общее | 270,84 | - | - | - | |
| Повторений | 3,33 | - | - | - | |
| Вариантов | 251,72 | 83,91 | 47,95 | 3,86 | |
| Остаточное (ошибочное) | 15,79 | 1,75 | - | - |
Дисперсия – это средний квадрат отклонений, вычисляется она по формуле:
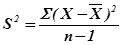 ,
,
где Σ(X– 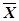 )2 – сумма квадратов отклонений отдельных показателей от их средней арифметической;
)2 – сумма квадратов отклонений отдельных показателей от их средней арифметической;
n – 1 или v – число степеней свободы.
Сумму квадратов отклонений, вычисленную ранее, проставляют на соответствующее место в таблице.
Число степеней свободы находят вычитанием единицы из общего числа данных, на основании которых была вычислена сумма квадратов отклонений. Общее варьирование вычисляется для всех делянок, в нашем примере на основании 16 показателей (число делянок в опыте N = ln = 4 х 4 = 16). Отсюда число степеней свободы общего варьирования Vy = ln – 1 = 16 – 1 = 15. Число степеней свободы для повторений Vp = n – 1 = 4 – 1 = 3, для вариантов Vy = 1 – 1 = 4 – 1 = 3.
Число степеней свободы для остаточного варьирования, как и само остаточное варьирование, определяется как остаток:
Vz = Vy – Vp – Vv = 15 – 3 – 3 = 9.
Теперь вычисляют дисперсии вариантов и остаточную.
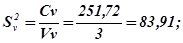
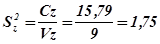 .
.
Правильность вычисления исходных данных для таблицы дисперсионного анализа и расчетов в самой таблице (исключая критерий F) можно проверить по уравнению:
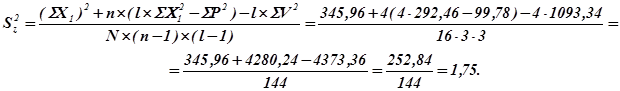
Полученный по проверочному уравнению результат совпал с ранее найденной обычным способом остаточной дисперсией, что свидетельствует о безошибочности расчетов.
6. Оценка существенности влияния вариантов на урожай в опыте. Это делается путем проверки нулевой гипотезы Н0 с помощью критерия F. Мы предполагаем, что изучаемые в опыте варианты не оказывали влияния на урожай, а наблюдаемые различия в поделяночных урожаях вызваны случайными причинами. Иными словами, мы представляем дело так, как если бы опытный участок засеяли одной культурой при одинаковой агротехнике, затем разбили его на делянки и повторения и учли урожай такого фиктивного «опыта».
В этом случае дисперсии вариантов и остаточная представляли бы собой дисперсии двух выборок из одной и той же генеральной совокупности – урожая всего опытного участка. Но согласно закону нормального распределения эти дисперсии могут отличаться друг от друга под действием случайных причин не более чем на определенную величину. Если же фактические расхождения между двумя дисперсиями выходят за эти пределы, они не принадлежат одной и той же генеральной совокупности, и нулевая гипотеза отбрасывается, различия между вариантами опыта признаются существенными, неслучайными, и наоборот.
При дисперсионном анализе оценка существенности влияния вариантов опыта на урожай производится путем сопоставления критерия F фактического, вычисленного на основании данных опыта и показывающего фактическое расхождение между дисперсиями, с F табличным, или теоретическим, показывающим пределы возможных расхождений между дисперсиями выборок из одной и той же генеральной совокупности. Значение Fтеорет. отыскивают в соответствующей таблице при заданном уровне вероятности (обычно 95%) на пересечении двух граф: «Число степеней свободы для большей дисперсии», т.е. вариантов vv, и «Число степеней свободы для меньшей дисперсии», т.е. остаточной vz. Fфакт. определяют по отношению:
Fфакт. = 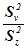 .
.
Если Fфакт. ≥ Fтеорет., то влияние вариантов на урожай в данном опыте признается существенным и Н0 отвергается. В противном случае (когда Fфакт. < Fтеорет.) делается вывод о том, что влияние вариантов на урожай математически не доказано. В таком случае ограничиваются определением ошибки опыта и дальнейшую статистическую обработку не производят.
Внимание! Для приобретения практических навыков при выполнении задания дальнейшие вычисления производите независимо от величины критерия F.
В нашем примере Fфакт.. 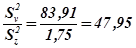 . Fфакт. Для 5%-ного уровня значимости при vv = 3 и vz = 9 равно 3,86.
. Fфакт. Для 5%-ного уровня значимости при vv = 3 и vz = 9 равно 3,86.
Fтабл. показывает, во сколько раз в данном случае дисперсия вариантов должна превышать остаточную, чтобы была доказана существенность влияния вариантов. В нашем опыте Fфакт. > Fтабл. (дисперсия вариантов превышает остаточную в 47,95 раза) и, следовательно, действие изученных вариантов (агроприемов или сортов) статистически доказано.
7. Определение ошибки (точности) опыта S 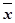 %. Это статистический показатель характеризует процент колебаний урожаев в опыте под действием случайных причин. Чем сильнее случайные колебания поделяночных урожаев (главным образом из-за пестроты плодородия земельного участка), тем опыт менее точен и тем более его ошибка. Чем точнее опыт, тем меньшие различия между вариантами можно уловить с его помощью. Напротив, если точность опыта низка, возрастает риск пройти мимо перспективных агроприемов, так как их влияние на урожай в опыте будет смазано, затушевано действием случайных причин.
%. Это статистический показатель характеризует процент колебаний урожаев в опыте под действием случайных причин. Чем сильнее случайные колебания поделяночных урожаев (главным образом из-за пестроты плодородия земельного участка), тем опыт менее точен и тем более его ошибка. Чем точнее опыт, тем меньшие различия между вариантами можно уловить с его помощью. Напротив, если точность опыта низка, возрастает риск пройти мимо перспективных агроприемов, так как их влияние на урожай в опыте будет смазано, затушевано действием случайных причин.
При оценке точности полевых агротехнических опытов обычно пользуются такой примерной шкалой:
S 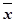 % ≤ 2% – точность опыта отличная;
% ≤ 2% – точность опыта отличная;
2-3% – хорошая;
3-5% – вполне удовлетворительная;
5-7% – удовлетворительная;
>7% – неудовлетворительная.
В опытах по сортоиспытанию, где различия между испытуемыми сортами по урожайности иногда незначительны, ошибка не должна превышать 4%.
Если ошибка проведенного опыта оказывается слишком высокой, он становится бесполезным, и исследователь должен принять меры к уменьшению влияния случайных факторов, улучшить методику постановки опыта (подобрать более выравненный по плодородию участок, правильно выбрать площадь, форму делянок и разместить их, увеличить повторность опыта, более тщательно и единообразно проводить полевые работы, учет урожая и т.д.).
Относительная ошибка средней арифметической (точность опыта) вычисляется по формуле:
S 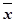 % =
% = 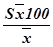 ,
,
где S 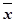 % – ошибка средней арифметической (абсолютная);
% – ошибка средней арифметической (абсолютная);
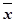 – средний урожай в опыте.
– средний урожай в опыте.
В свою очередь S 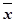 =
= 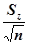 или
или 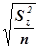 ,
,
где 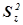 – остаточная дисперсия;
– остаточная дисперсия;
n – повторность опыта.
В нашем примере
S 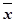 =
= 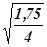 =0,66 ц/га; S
=0,66 ц/га; S 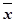 % =
% = 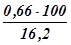 =4,1%.
=4,1%.
Точность опыта оценивается как вполне удовлетворительная.
8. Оценка различий между вариантами опыта. Это заключительный этап дисперсионного анализа. Он производится, если Fфакт. ≥ Fтабл..
Критерий F оценивает совокупное действие изучаемых вариантов на урожай. Когда Fфакт. ≥ Fтабл., это означает, что в целом варианты опыта оказали заметное, существенное влияние на урожай в опыте. Однако о действии каждого отдельного варианта судить пока нельзя, так как при существенном суммарном влиянии вариантов частные различия между некоторыми из них могут оказаться недостоверными.
Поэтому после определения существенности совокупного действия вариантов необходимо оценить достоверность частных различий между урожаями вариантов. Существенность частных различий между вариантами опыта при дисперсионном анализе определяется с помощью критерия НСР.
НСР – это наименьшая существенная разность, т.е. та минимальная разница между урожаями, которая в данном опыте является достоверной, математически доказанной. Она рассчитывается при уровне значимости, с которым взято Fтабл., обычно 5% (0,05), по формуле:
НСР = tSd,
где t – критерий Стьюдента. Он берется из таблицы при числе степеней свободы остаточной дисперсии (vz) и заданном уровне значимости. В нашем примере при числе степеней свободы 9 и 5-%-ном уровне значимости он составляет 2,26;
Sd – ошибка разности в опыте.
Общая формула ошибки разности средних арифметических имеет вид:
Sd = 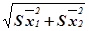 .
.
При дисперсионном анализе для всего опыта вычисляют одну обобщенную ошибку средней арифметической
(S 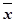 =
= 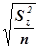 ),
),
и поэтому S 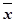 1 и S
1 и S 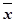 2.
2.
Отсюда Sd = 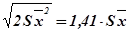 или Sd =
или Sd = 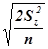 .
.
В нашем опыте Sd = 1,4 · 0,66 = 0,93 ц/га, а НСР05 =t05 · 0,93 = 2,26 · 0,93 = 2,1 ц/га.
Величину НСР сопоставляют с отклонениями урожаев отдельных вариантов от контроля. НСР показывает возможные случайные колебания урожаев по вариантам. Скажем, если НСР = 2,1 ц/га, то это означает, что в данном опыте под влиянием случайных причин урожаи вариантов могут колебаться в пределах ± 2,1 ц/га. Когда фактические различия между вариантами выходят за эти пределы, то перед нами уже не случайные, а закономерные явления и сравниваемые между собой варианты существенно отличаются по урожайности друг от друга. При помощи НСР можно сравнивать изучаемые варианты не только с контролем, но и между собой.
Для наглядного и компактного представления полученных при дисперсионном анализе данных в заключение составляют итоговую таблицу. В нее обычно заносят средние урожаи по вариантам опыта и их отклонения от контроля, а также два основных статистических показателя: точность опыта и НСР. В сортоиспытании, а иногда и в агротехнических опытах все варианты (сорта, агроприемы) для наглядности подразделяют на три группы.
I группа – варианты, существенно превышающие по урожайности контроль (отклонения от контроля имеют положительный знак и по абсолютной величине больше НСР).
II группа – варианты, для которых разница с контролем статистически недоказана (отклонения не выходят за пределы ± НСР).
III группа – варианты, уступающие по урожайности контролю (отклонения от контроля имеют отрицательный знак и по абсолютной величине больше НСР).
В нашем опыте урожай по варианту 2 составил 22,6 ц/га, что превышает урожай контроля – варианта I на 6,6 ц/га (22,6 ц/га – 16,0 ц/га). Эта разница больше, чем НСР, которая для данного опыта равна 2,1 ц/га. Следовательно, второй вариант превзошел по своей урожайности контроль и относится к группе I. Вариант 3 следует считать равноценным контролю, так как разность (2,0 ц/га) по абсолютной величине не превышает НСР и может быть вызвана случайными причинами. Что касается последнего, четвертого варианта, то он существенно уступает контролю и относится к группе III: отклонение (–4,0 ц/га) имеет отрицательный знак, а по абсолютной величину превышает НСР.
Дата добавления: 2021-01-11; просмотров: 1207;











