Структурні моделі цифрових автоматів

Нагадаємо, що автомат, значення виходів (Z) якого залежать не тільки від значень входів (X) в даний момент часу, але і від його стану, називається послідовністним, або автоматом з пам'яттю.

Канонічний метод синтезу автоматів зводить завдання їх структурного синтезу до реалізації однієї або двох комбінаційних схем, перша з яких охоплена зворотними зв'язками.

Для того щоб розрізнити поточний і наступний моменти часу, в моделі автоматів вводяться «однотактні» елементи затримки (ЕЗ), або тригери, які відрізняються від функціональних елементів затримки, що використовуються в керуючих автоматах для реалізації часових інтервалів необхідної тривалості.

Залежно від того, де в автоматах розташовуються ЕЗ, вони розбиваються на два підкласи.

В автоматах першого роду елементи затримки розташовуються безпосередньо в ланцюзі «вхід-вихід», а в автоматах другого роду вони розміщується в колі зворотного зв'язку. Тому, якщо в автоматах першого роду вихідні сигнали запізнюються на такт в порівнянні з вхідними сигналами, то в автоматах другого роду запізнювання практично відсутнє.

Структурна схема автомата без вихідного перетворювача першого роду представлена на рис. 5.4, другого роду – на рис. 5.5. На цих схемах символом « » позначені ЕЗ.

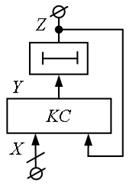
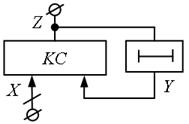
Рис.5.4. Рис.5.5.

Будемо використовувати наступні позначення змінних: X – вхідні змінні; Y – внутрішні змінні; Z – вихідні змінні. Ці позначення носять мнемонічний характер, тому що згадуються в тому ж порядку, як і в латинському алфавіті.

Виходячи з викладеного для автоматів розглянутого класу можуть бути використані наступні математичні моделі:

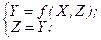
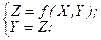
Моделі автоматів без вихідного перетворювача (АБВП) не є універсальними, тому що при їх використанні коди станів автомата примусово повинні збігатися з кодами вихідних змінних, що можливо лише в тих випадках, коли в графі переходів відсутні різні вершини з однаковими комбінаціями значень вихідних змінних.

Окремим випадком АБВП є автомати без виходу (АБВ). Їх структура збігається зі структурою автоматів, що представлені на рис. 5.4 і рис. 5.5, проте в зовнішнє середовище вони видають не вихідні змінні Z, а внутрішні змінні Y. Використання цього підкласу автоматів може різко спростити опис композицій автоматів.

Якщо в різних станах автомат повинен видати однакові набори значень вихідних змінних, то для його реалізації може бути використана модель універсального АБВП першого (рис. 5.6) або другого (рис. 5.7) роду.

Універсальність цих моделей досягається за рахунок кодування станів автомата, що дозволяє розрізняти стани, в тому числі і з однаковими значеннями вихідних змінних. При цьому, одна частина кожної кодової комбінації примусово задається вектором значень вихідних змінних, а інша – довільно, за рахунок значень внутрішніх змінних, що вводяться з метою розрізнення станів з однаковими значеннями вихідних змінних.

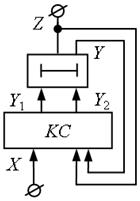
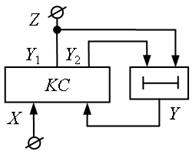
Рис.5.6 Рис.5.7.

Відмовитися від повного або часткового примусового кодування станів можливо при введенні в модель автомата другої комбінаційної схеми КС2, що здійснює перетворення вільно обраних кодів станів в набори значень вихідних змінних. Структурна схема автомата представлена на рис. 5.8. Цей автомат описуються наступним чином:

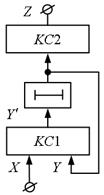
Рис.5.8.

Для автоматів Мура характерно, що його вихідні змінні залежать тільки від змінних станів і не залежать від вхідних змінних. Для ряду алгоритмів більш природним є реалізація автомата у вигляді автомата Мілі, для якого характерно, що його вихідні змінні залежать не тільки від змінних станів, але і від вхідних змінних (рис. 5.10, рис. 5.11).

Ці автомати першого і другого роду описуються наступним чином:

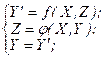
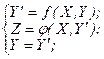
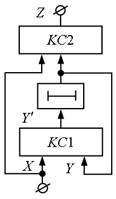
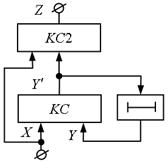
Рис.5.10 Рис.5.11.

Оскільки комбінаційна схема КС2 в автоматах Мілі отримує, на відміну від автоматів Мура, також і вхідну інформацію, можна стверджувати, що кількість станів автомата Мілі не перевищує числа станів еквівалентного йому автомата Мура.

Автомати Мура та Мілі першого і другого роду, у яких забезпечується запам'ятовування вихідних змінних, будемо називати автоматами із збереженням значень вихідних змінних.

Ці автомати можуть розглядатися також і як суперпозиція двох простих типів автоматів: автомата без виходу першого або другого роду і АБВП другого роду.

Можливі чотири структури автоматів розглянутого класу: два – на основі автоматів Мура (рис. 5.12, 5.13) і два – на основі автоматів Мілі (рис. 5.14, рис. 5.15).

Автомати Мура цього класу описуються співвідношеннями:

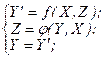
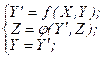
а автомати Мілі цього класу відповідно:

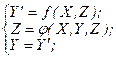
Відзначимо також і те, що існують автомати без вихідного перетворювача, що належать до класу автоматів із збереженням значень вихідних змінних.

У разі, якщо заданий алгоритм описано сукупністю автоматів, то в силу того, що при програмній реалізації вони виконуються послідовно, вихідний набір при цьому формується по частинах, що в загальному випадку може бути дуже небезпечним.

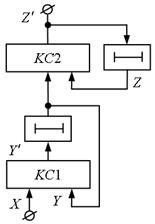
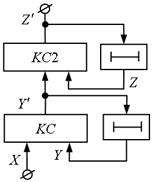
Рис.5.12. Рис.5.13.

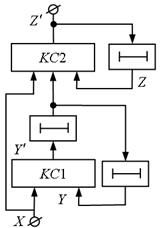
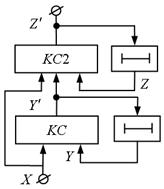
Рис.5.14 Рис.5.15

Модель сукупності автоматів без виходу із загальним вихідним перетворювачем представлена на рис. 5.16. При цьому, до спрацьовування останнього автомата сукупності, зберігається попередній вихідний набір, а після його спрацьовування загальний вихідний перетворювач формує новий набір. Таким чином, у запропонованій моделі, протягом перехідного процесу вихідний набір не змінюється, і лише після його завершення формується новий, що робить поведінку сукупності автоматів адекватною поведінці єдиного автомата.

У разі, якщо автомат заданий одним графом переходів, то кожна булева формула, що позначає дугу ГП, може бути реалізована незалежно. Однак, якщо всі булеві формули, що містять більш однієї змінної, позначати новими змінними, припускаючи, що однакові формули мають одне і те ж позначення, то з'являється можливість їх спільної мінімізації та формування загального вхідного перетворювача. Це дозволяє говорити про моделі автомата з загальним вхідним перетворювачем (рис. 5.17). Аналогічна модель може бути використана і у випадку, якщо алгоритм реалізується сукупністю автоматів.

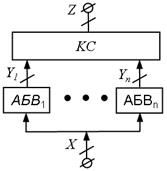
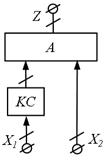
Рис.5.16. Рис.5.17.