Анализ сезонных колебаний
Под сезонными колебаниями понимается периодически повторяющееся из года в год повышение и снижение уровней в отдельные месяцы или кварталы.
Пример 8.11. Имеются следующие данные:
Таблица 8.19
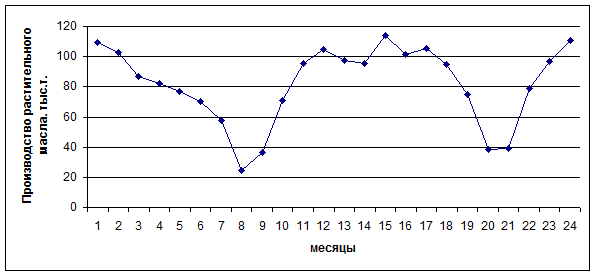
Производство растительного масла в России в 1992-1993 гг.
по месяцам, тыс. т.
| Год | Месяц | |||||||||||
| 109,5 | 102,7 | 86,6 | 82,3 | 76,6 | 70,0 | 57,6 | 24,5 | 36,3 | 70,7 | 95,2 | 104,5 | |
| 97,6 | 95,5 | 114,2 | 101,3 | 105,6 | 94,6 | 75,2 | 38,6 | 38,9 | 78,7 | 96,5 | 111,0 |
 |
Если выявленные колебания не случайны, то они сохранятся и на укрупненных интервалах, например, квартальных.
Таблица 8.20
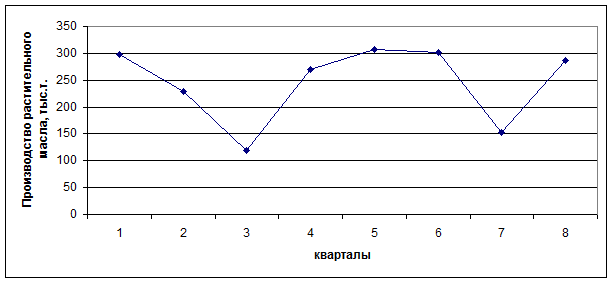
Производство растительного масла в России в 1992-1993 гг. по кварталам
| Год | ||||||||
| Квартал | I | II | III | VI | I | II | III | IV |
| Произведено | 298,8 | 228,9 | 118,4 | 270,4 | 307,4 | 301,5 | 152,7 | 286,2 |
При изучении рядов динамики, содержащих «сезонную волну», её выделяют из общей колеблемости уровней и измеряют. Существует ряд методов решения этой задачи. Для измерения «сезонной волны» рассчитывают либо абсолютные разности (отклонения) фактических уровней от среднего уровня, либо отношения месячных уровней к среднему уровню за год, так называемые индексы сезонности:
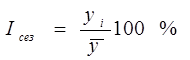
Пример 8.12. Произведем расчет индексов сезонности и абсолютных отклонений уровней от среднего на примере данных о производстве растительного масла в России в 1992 году.
Таблица 8.21
Сезонные колебания производства растительного масла в России в 1992 г.
| Месяц | Произ-водство масла, тыс.т. | Индекс сезонности, % к средне- месячному уровню | Абсолют- ное откло- нение от средне- месячного уровня | Абсолют- ное откло- нение, % к средне-месячному уровню | (Iсез -100%)2 | 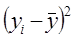
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| Январь | 109,5 | 143,4 | 33,125 | 43,4 | 1883,56 | 1097,266 |
| Февраль | 102,7 | 134,5 | 26,325 | 34,5 | 1190,25 | 693,006 |
| Март | 86,6 | 113,4 | 10,225 | 13,4 | 179,56 | 104,551 |
| Апрель | 82,3 | 107,8 | 5,925 | 7,8 | 60,84 | 35,106 |
| Май | 76,6 | 100,3 | 0,225 | 0,3 | 0,09 | 0,051 |
| Июнь | 70,0 | 91,7 | -6,375 | -8,4 | 68,89 | 40,641 |
| Июль | 57,6 | 75,4 | -18,775 | -24,6 | 605,16 | 352,501 |
| Август | 24,5 | 32,1 | -51,875 | -67,9 | 4610,41 | 2691,017 |
| Сентябрь | 36,3 | 47,5 | -40,075 | -52,5 | 2756,25 | 1606,006 |
| Октябрь | 70,7 | 92,6 | -5,675 | -7,4 | 54,76 | 32,206 |
| Ноябрь | 95,2 | 124,6 | 18,825 | 24,6 | 605,16 | 354,381 |
| Декабрь | 104,5 | 136,8 | 28,125 | 36,8 | 1354,24 | 791,016 |
| Итого | 916,5 | 1200,1 | 12270,84 | 7797,747 |
Средний месячный уровень за год: 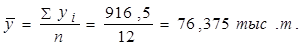
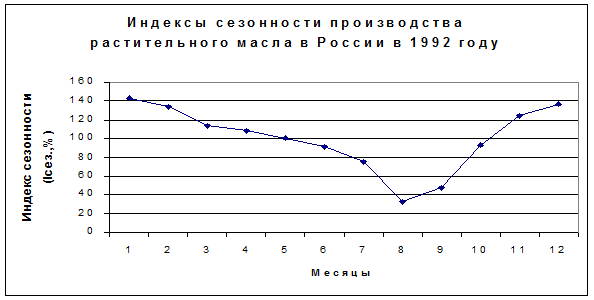
Графическое изображение индекса сезонности наглядно показывает форму, характер сезонной волны, относительно среднемесячного уровня за год, принимаемого за 100%.
Для характеристики силы колеблемости уровней ряда динамики из-за сезонной неравномерности используется среднее квадратическое отклонение индексов сезонности (в процентах) от 100%
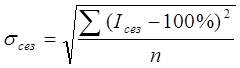
Для примера 8.12: 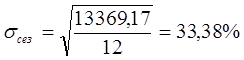
Этот же результат можно получить и по-другому, как коэффициент вариации (колеблемости):
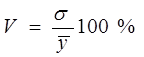 , где
, где 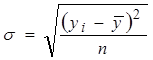 - среднее квадратическое отклонение.
- среднее квадратическое отклонение.
Для примера 8.12 сумма квадратов отклонений рассчитана в графе 7 таблицы 8.21, среднее значение уровня 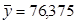 , отсюда
, отсюда 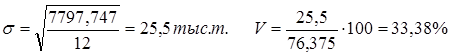 , т.е. результаты двух показателей
, т.е. результаты двух показателей 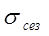 и V - идентичны.
и V - идентичны.
Расчет индексов сезонности за ряд лет можно осуществить двумя способами.
Первый способ состоит в определении простой средней за одни и те же месяцы изучаемого периода и сопоставлении их со средней за весь изучаемый период.
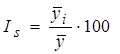 %
%
Второй способ заключается в том, что в начале вычисляют по каждому году индексы сезонности, а затем из индексов одноименных месяцев находится средняя арифметическая, которая и является индексом сезонности.
Пример 8.13. По данным о производстве растительного масла в 1992 и 1993 году рассчитаем индекс сезонности первым (табл. 8.22) и вторым (табл. 8.23) способами.
Таблица 8.22
Дата добавления: 2021-12-14; просмотров: 498;











