Електричні кола однофазного змінного струму.

Вироблення, передача використання електричної енергії виконується в основному за допомогою пристроїв та установок змінного струму. Для цього використовують генератори трансформатори, лінії електропередач та розподільчі мережі змінного струму. Широко використовуються приймачі змінного струму.

Змінним електричним струмом називається електричний струм, який протягом певного часу змінюється за величиною та напрямком.

В лінійних електричних колах змінний синусоїдальний струм виникає під дією е.р.с. такої ж форми, тому спочатку проаналізуємо е.р.с.

Аналіз електричних кіл змінного струму неможливо здійснити без вираження е.р.с. струмів, напруг їхніми рівняннями, а для наочності застосовують графіки цих величин.

За даними рівняннями визначається залежність е.р.с. від часу.

З рівняння та графіку синусоїдної величини можна визначити амплітуду, кутову частоту, початкову фазу, період, частоту, для будь-якого моменту часу миттєве значення.

Означення поширюються на всі величини, які змінюються за синусоїдним законом (струм, напруга та інше).

Миттєве значення е.р.с – це е.р.с. у розглядуваний момент часу миттєве е.р.с. визначається рівнянням:

при підстановці в нього часу t, який минув від початку відліку до заданого моменту.

Період Т – найменший інтервал часу із закінченням якого миттєве значення періодичної е.р.с. повторюється.

Частота f – величина, обернена періоду

,

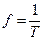тобто частота дорівнює кількості періодів змінної е.р.с. за секунду. Час тому виражають в герцах (Гц) 1/с

Амплітуда Еm – найбільше значення, якого набуває е.р.с. протягом періоду. Амплітуда є однією з миттєвих величин.

Фаза (фазовий кутωt + φ) – аргумент синусоїдної е.р.с., який відлічують від найближчої попередньої точки переходу е.р.с. через нуль до додатного значення.

Початкова фаза – фаза синусоїдної е.р.с. у початковий момент часу. Дві синусоїдні величини, які мають різні початкові фази, називаються зсунутими за фазою .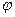

Кутова частота – швидкість зміни фази. За час одного періоду Т фазовий кут рівномірно змінюється на 2π, тому

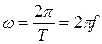
Діюче значення синусоїдної величини

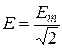
це його середнє квадратичне за період.

При розрахунку електричних кіл змінного струму користуються простим і наочним способом графічного зображення синусоїдних величин за допомогою обертових векторів.

Додатній напрямок обертання векторів прийнято проти годинникової стрілки. Тому на векторній діаграмі (рис. 21) кут утворений вектором Е, і позитивною віссю х вважається позитивним.

Миттєве значення е.р.с.

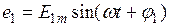
Кут, утворений вектором Е2 і позитивною віссю х, вважається негативним. Миттєве значення е.р.с.

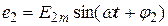
Сукупність векторів, які зображують на одному рисунку кілька синусоїдних величин однакової частоти в початковий момент часу, називається векторною діаграмою.

Електричне коло змінного струму характеризується трьома параметрами: активним опором R, ємністю С, індуктивністю L.

Лампи розжарювання, побутові нагрівальні прилади та реостати мають активний опір R. Коло не навантаженого трансформатора можна розглядати як індуктивність L, а кабельна лінія без навантаження – як ємність С.

1. Коло з активним опором

В колі електрична енергія перетворюється на теплову.

Вираз для миттєвого струму знаходиться за законом Ома

де 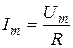- амплітуда струму.

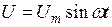- миттєве значення напруги.

З рівнянь видно, що початкові фази напруги і струму однакові, тобто напруга і струм у колі з активним опором співпадають за фазою.

Якщо виразити миттєві значення напруги та струму через діючі значення, то рівняння закону Ома нічим не відрізняється від формул для кола постійного струму.

Рис.23

; ;

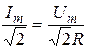
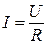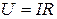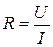
Миттєва потужність дорівнює добуткові миттєвих значень напруги і струму:

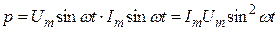
Активна потужність кола дорівнює добуткові діючих значень напруги і струму

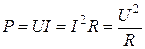(Вт)

2. Коло з індуктивним опором

Активним опором нехтуємо (не навантажений трансформатор). В колі відома індуктивність і струм, який змінюється за законом:

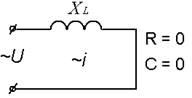
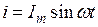
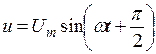
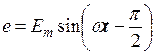
В колі з котушкою індуктивності напруга випереджає струм по фазі на 90˚(рис. 25 а, б)

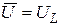
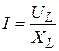, (А)

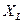реактивний опір індуктивності, або індуктивний опір

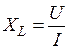, (Ом)

Реактивний опір це розрахункова величина і введена вона для полегшення розрахунків

В колі з котушкою індуктивності активна потужність за період дорівнює нулю Р=0, так як в колі з індуктивністю перетворення електричної енергії в інші види енергії (теплову, механічну) не відбувається. Існує реактивна потужність

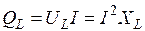, (вар)

Одиниця виміру (вар) – вольт-ампер реактивний.

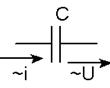
3. Коло з ємністю

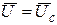R = 0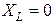

В конденсаторі з ідеальним діелектриком припускаємо повну відсутність струму провідності і втрат енергії. Зміна напруги між обкладинками конденсатора супроводжується електричним струмом зміщення, величина якого залежить від ємності конденсатора. Напруга на конденсаторі

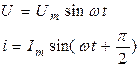
З рівнянь, векторної і хвильової діаграми (рис. 27 а, б) видно, що струм випереджає напругу на кут 90˚

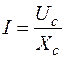, (А)

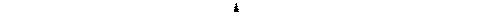
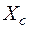- реактивний опір ємності або ємнісний опір

Ємнісний опір – величина, обернена добутку ємності та кутової частоти

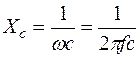, (Ом)

Активна потужність в колі з ємністю дорівнює нулю, так як не відбувається перетворення електричної енергії в інші види енергії.

Реактивна потужність дорівнює

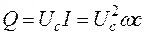, (вар)

4. Коло з реальною котушкою індуктивності

В колі з послідовним з’єднанням елементів реальна котушка характеризується активним опором R та індуктивністю L (рис.28)

Слід зауважити, що коло, яке розглядаємо (R, L) в більшості випадків являють собою котушку електричної машини, апарата чи приладу.

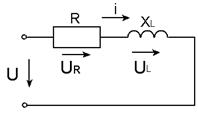
Рис. 28

Реальна котушка відрізняється від ідеальної тим, що змінний струм у ній супроводжується не тільки зміною енергії в магнітному полі, а й перетворенням електричної енергії в теплову.

При розрахунку даного кола (рис. 28) слід виходити з того, що опори з’єднані послідовно. При цьому один і той же струм проходить по всіх елементах електричного кола, а напруга розподіляється на активному і реактивному опорах. Тому миттєві значення струмів та напруг виражені рівнянням.

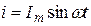
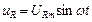
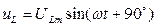
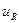- миттєве значення напруги на активному опорі

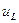- миттєве значення напруги на індуктивному опорі.

Скористаємося векторним способом додавання векторних величин для побудови векторної діаграми реальної котушки індуктивності. Вектор загальної напруги.

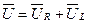
За початковий вектор діаграми беремо вектор струму (рис.29а)

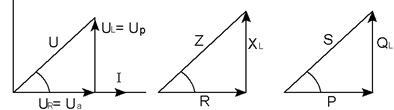
Рис. 29

Напрямок цього вектора збігається з додатнім напрямом осі, від якої відмічають фазові кути (початкова фаза заданого струму )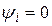

Вектор 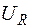за напрямком збігається з вектором струму І, а вектор 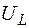направлений перпендикулярно до струму І з додатним кутом.

З діаграми видно, що вектор загальної напруги U дорівнює гіпотенузі прямокутного трикутника, катетами якого є вектори спадів напруги на активному та індуктивному опорах , .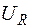

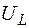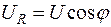
Проекцією вектора U на напрямок, вектора струму називають активною складовою вектора напруги і позначають 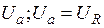(для котушки)

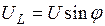
Проекцією вектора U на напрямок перпендикулярний до вектора струму, називається реактивна складова напруги і позначається .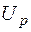

Для котушки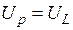

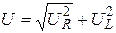
При струмі

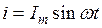
рівняння напруги можливо записати на основі векторної діаграми

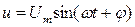
Сторони трикутника напруг, виражені в одиницях напруги, поділимо на струм І. Отримаємо трикутник опорів. (рис. 29 б) катетами якого є активний 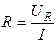та індуктивний 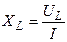опори, а гіпотенузою .

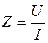Відношення діючої напруги до діючого струму даного кола називається повним опором. Сторони трикутника опорів не можна вважати векторним, так як опори не являються функціями часу.

З трикутника опорів випливає: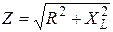

З трикутника напруг і опорів визначаємо:

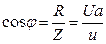
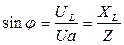
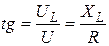
Миттєва потужність котушки:

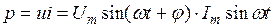
З графіка миттєвої потужності (рис. 30) видно, що протягом періоду потужність чотири рази змінює знак; відповідно напрям потоку енергії в даному випадку протягом періоду змінюється.

При додатному значенні потужності енергія переходить від джерела до приймача, а при від’ємному – навпаки.

Швидкість необоротного процесу перетворення енергії оцінюється середньою потужністю за період, чи активною потужністю Р. Швидкість обмінного процесу характеризується реактивною потужністю Q.

На основі раніше викладеного матеріалу в активному опорі 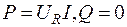, а індуктивному .

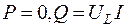Активна потужність всього кола дорівнює активній потужності в опорі К, а реактивна – реактивній потужності в індуктивному опорі 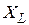. Підставляючи значення 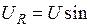, які визначають з трикутника напруг (рис. 29 а) по формулах отримаємо:

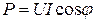
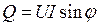
Крім активної і реактивної потужності використовують поняття повна потужність S, яка визначається добутком діючих величин напруги і струму кола:

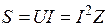
Значення повної потужності можна визначити через активну та реактивну потужності:

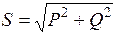
Потужності S,P,Q графічно можна зобразити сторонами прямокутного трикутника (рис. 29 в) трикутник потужностей виходить з трикутника напруг, якщо сторони останнього, виражені в одиницях напруг, помножити на струм.

З трикутника потужностей можна визначити

; ;

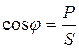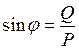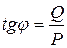
Відношення активної потужності кола до її повної потужності 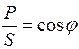називається коефіцієнтом потужності.

Розглянемо електричне коло з реальною котушкою індуктивності та конденсатором.

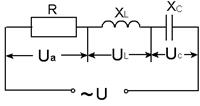
Рис. 31

Для даного електричного кола миттєві значення струму та напруги запишемо

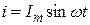
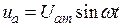
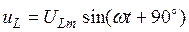
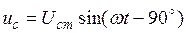
Миттєву величину загальної напруги можна визначити як суму миттєвих напруг на окремих елементах.

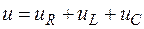
Маючи на увазі неспівпадання за фазою активних і реактивних напруг, загальна напруга виходить векторним складанням

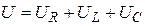
В залежності від співвідношень величини реактивних опорів індуктивності та ємності можна виділити три випадки:

1.

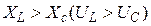
Вектори реактивних складових напруг направлені по одній прямій в протилежні напрямки, тому їм дають різні знаки: реактивна напруга індуктивності буде позитивною, а напруга ємності – негативною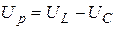

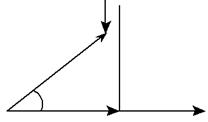
Рис. 32

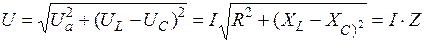
Реактивний опір носить індуктивний характер

2. 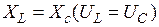(резонанс напруг)

В цьому випадку реактивна складова напруги котушки і конденсатора рівні за величиною і взаємо компенсовані.

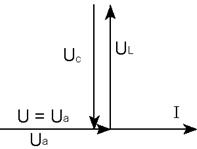
Рис. 33

Реактивні складові загальної напруги та загального опору (реактивного) дорівнюють нулю. Повний опір Z=R. Загальна напруга співпадає по фазі зі струмом і дорівнює за величиною активній складовій напруги. Кут φ зсуву фаз між струмом і загальною напругою дорівнює нулю. Струм в колі і загальна напруга зв’язані формулою U= IR, чи .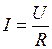

3.

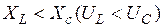
Загальна напруга відстає від струму на кут φ <0.

Реактивний опір кола носить ємнісний характер. Для розрахунку використовують формули з першого випадку

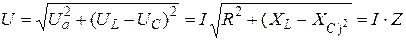
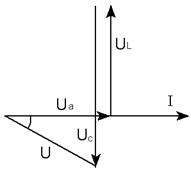
Рис. 34

З трикутників напруг легко отримати трикутник потужностей, з якого випливають уже відомі формули

;

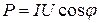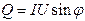
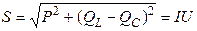
Реактивні потужності входять в розрахунки також з різними знаками: індуктивна потужність позитивна, а ємнісна негативна.

Повна потужність завжди позитивна.