Преобразования Лоренца

Постулаты Эйнштейна требовали коренного пересмотра представлений о свойствах пространства, времени и движения. Покажем это на простом примере.

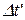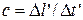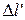Представим себе, что движущейся системой отсчета K', является поезд. Пусть в момент, когда его хвостовой вагон поравнялся со стрелочником (система отсчета K), стоящим на насыпи, из этого вагона был послан световой сигнал машинисту. Через время машинист этот сигнал регистрирует, тогда скорость света , где – длина поезда в системе K'.

Обозначим через 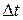время, отсчитываемое стрелочником. Что касается пути, пройденного светом с точки зрения стрелочника, то он состоит из длины поезда 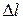, движущегося со скоростью V,и расстояния Vdt, на которое за время 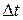хвостовой вагон отъедет от стрелочника.

Итак, с точки зрения стрелочника .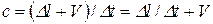

Очевидно, что 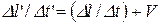(7)

несовместимо с условиями .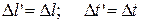

Нужно либо считать, что 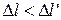, т. е. поезд с точки зрения стрелочника стал короче, либо время 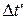в движущейся системе идет медленнее, т. е. 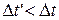. Оказывается, имеет место и то и другое одновременно.

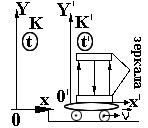Покажем, что движущиеся часы идут медленнее. Для этого рассмотрим две инерциальные системы отсчета K и K'. Систему K будем считать покоящейся, а систему K' – движущейся со скоростью V, (см. рис. 2).

Рис. 2

Предположим, что в системе K находятся часы в виде двух параллельных зеркал и источника света. Они неподвижны в системе K'. Свет включается на короткое время и начинает двигаться вверх и вниз, попеременно отражаясь от верхнего и нижнего зеркал, (см. рис. 2.). В таких часах качающимся маятником является луч света.

Рассмотрим один из полупериодов, когда свет движется сверху вниз. Пусть с точки зрения наблюдателя системы K' это происходит за время Dt', тогда расстояние между зеркалами будет 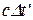, причем оно будет поперечным, как по отношению системы K', так и системы K, и поэтому одинаковым в этих системах. Однако с точки зрения наблюдателя системы K свет распространяется наклонно, т. е. свет будет снесен вправо на расстояние VDt.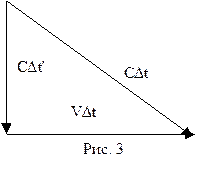

Из рис. 3 по теореме Пифагора находим 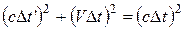, откуда

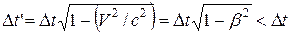, (8)

где 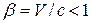, т. е. движущиеся часы идут медленнее, чем неподвижные.

Подтверждением этого служит время жизни движущихся мюонов; собственное время их жизни 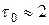мкс, а по часам неподвижным относительно Земли - значительно больше:

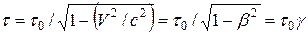, (9)

где V – скорость мюона относительно Земли, 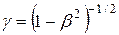– коэффициент Лоренца, .

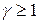Подобным образом можно показать, что размеры тел в направлении движения сокращаются, т. е.

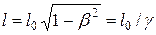. (10)

Исходя из двух постулатов, Эйнштейн в 1905 г. вывел преобразования Лоренца (полученные Лоренцом в 1904 г. как преобразования, по отношению к которым уравнения классической микроскопической электродинамики – уравнения Лоренца- Максвелла сохраняют свой вид).

Напишем их подобно преобразованиям Галилея:

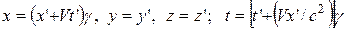, (11)

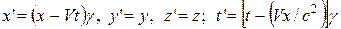. (12)

Для медленных движений, когда 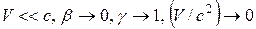преобразования Лоренца переходят в преобразования Галилея. Используя соотношения (11), (12), можно показать, что пространственные расстояния при преобразованиях Лоренца изменяются, т. е. 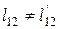, где

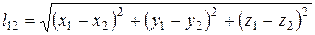(13)

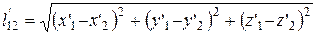. (14)

Этот эффект называется лоренцевым сокращением длины.

Неизменным (инвариантным) при преобразованиях Лоренца остается так называемый интервал между событиями

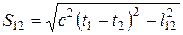.(15)