Таким образом, если разбить плоское движение тела на поступательное со

скоростью центра масс V_c и вращательное с угловой скоростью w вокруг оси, проходящей через центр масс тела, то кинетическая энергия распадается на два независимых слагаемых, одно из которых определяется только скоростью центра масс V_c, а другое – угловой скоростью w.

Из (13) следует, что при вращении тела относительно оси z, проходящей через центр масс С, его кинетическая энергия 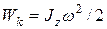. (14)

Работа и мощность при вращательном движении

При повороте тела на малый угол 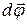вокруг оси Z совершается работа

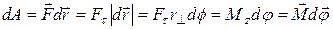. (15)

Мощность

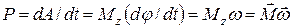. (16)

Сопоставим основные величины и уравнения поступательного и вращательного движений

Т А Б Л И Ц А № 1

ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ	ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ
Масса	m	момент инерции	J
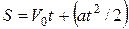
Путь	S	угол поворота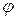
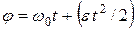
Скорость		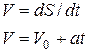угловая скорость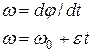
касательное ускорение		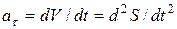угловое ускорение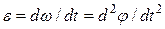
Сила		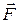момент силы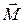
уравнение движения		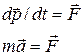уравнение движения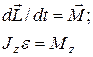
кинетическая энергия		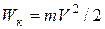кинетическая энергия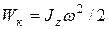
элементарная работа		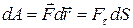элементарная работа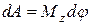
мощность		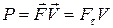мощность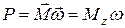

Л Е К Ц И И №№ 8 - 1 0 . П Р И Н Ц И П О Т Н О С И Т Е Л Ь Н О С Т И