Уравнение движения и равновесия твердого тела

Так как твердое тело является механической системой с шестью степенями свободы, то для описания его движения требуется шесть независимых числовых уравнений или два независимых векторных уравнения.

Одно из них – это уравнение движения центра масс С

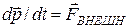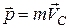, где . (1)

Второе – уравнение моментов

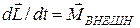. (2)

Если твердое тело покоится, то уравнения (1) и (2) переходят в

. (3)

Это необходимые условия равновесия твердого тела. Но они не являются достаточными. При их выполнении центр масс может двигаться прямолинейно и равномерно с произвольной скоростью, а само тело может вращаться с сохранением момента импульса. Такое движение твердого тела называют свободным. Следует отметить, что даже свободное движение твердого тела может быть очень сложным. Поэтому сначала рассмотрим простейший случай движения твердого тела.

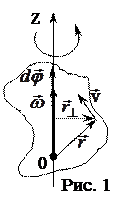7.4. Вращение твердого тела вокруг неподвижной оси

Движение твердого тела, при котором все точки прямой АВ, жестко связанной с телом, остаются неподвижными, называется вращением тела вокруг неподвижной оси АВ.

Такое твердое тело имеет одну степень свободы и его положение в пространстве полностью определяется значением угла поворота вокруг оси вращения из некоторого, условно выбранного, начального положения этого тела. Мерой перемещения тела за малый промежуток времени dt полагают вектор 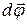элементарного поворота тела. По модулю он равен углу поворота тела за время dt, а его направление совпадает с направлением поступательного движения правого буравчика, направление вращения рукоятки которого совпадает с направлением вращения тела (рис. 1). Вектор угловой скорости 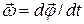. (4)

Если 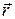– радиус вектор, проведенный из некоторой точки О на оси вращения ОZ до произвольной материальной точки тела, то скорость этой точки определяется соотношением 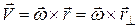, (5)

где 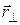– составляющая вектора 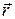, перпендикулярная оси, т.е. 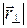– кратчайшее расстояние от оси до материальной точки.

Уравнение динамики тела, вращающегося вокруг неподвижной оси z, имеет вид

dL_z/dt = M_zВНЕШН, (6)

где 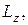M_zВНЕШН – проекции моментов импульса 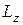и момента силы M_zВНЕШН на ось вращения z. Выведем другое выражение для уравнения (6). Определим момент импульса относительно точки О, лежащей на оси ОZ (см. рис. 2), полагая 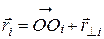, где 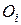– центр окружности, по которой движется i-я материальная точка твердого тела, тогда

.

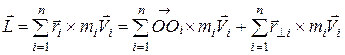Первое слагаемое перпендикулярно оси ОZ, а второе параллельно, так как .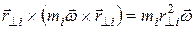

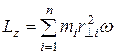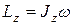Таким образом или , (7)

где величина

Рис. 2

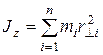(8)

называется моментом инерции тела относительно оси Z .

Тогда уравнение динамики тела, вращающегося относительно неподвижной оси Z [см. (6)], можно записать в виде 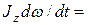M_zВНЕШН или 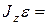M_zВНЕШН. (9)

Теорема Штейнера

В механике твердое тело обычно рассматривают как механическую систему, масса т которой непрерывно распределена по объему V тела, так что при вычислении момента инерции тела, суммирование в формуле (8), переходит в интегрирование

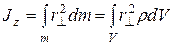, (10)

где 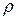– плотность тела, 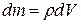– масса малого элемента объема dV, отстоящего от оси вращения тела на расстоянии .

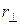Пример:

Расчет момента инерции однородного цилиндра относительно его геометрической оси Z.

Мысленно разделим цилиндр высоты h и радиуса R на концентрические слои толщиной dr. Если плотность материала цилиндра 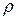, то масса dm , заключенная в слое dr; будет равна: 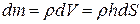; так как 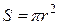, , 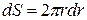то .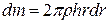

Используя формулу (10), находим момент инерции однородного цилиндра:

,

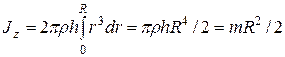где 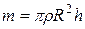– масса цилиндра.

Подсчет момента инерции тела относительно произвольной оси облегчается, если воспользоваться теоремой Штейнера:

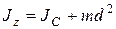, (11)

где 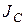– момент инерции тела относительно оси, проходящей через центр масс тела и параллельной оси Z; d – расстояние между осями.