Упражнение 18.4. Аналитические вычисления
Задача 1.На приведенной схеме сопротивление RR является переменным. Определить, как меняется ток между точками Л и В в зависимости от величины этого сопротивления.

Анализ.Перенумеровав сопротивления в указанном порядке и воспользовавшись законами Кирхгофа, получим систему уравнений, позволяющую найти величины токов.
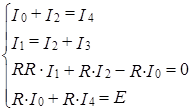
Эту систему надо решить, не подставляя конкретных значений вместо параметров R, RR и Е.
1. Запустите программу MathCad.
2. Введите ключевое слово given.
3. Введите уравнения системы, полученной в ходе анализа. Обозначьте неизвестные
токи переменными I0, I1, I2, I3, I4. Фиксированное сопротивление R обозначьте
переменной R0. Обратите внимание, что присваивать начальные значения токов
или задавать значения переменных R0, RR и E не требуется.
4. Введите функцию find, перечислив в качестве параметров неизвестные I0, I1, 12, I3, I4. Затем введите оператор аналитического вычисления, который выглядит как стрелка, направленная вправо, и вводится комбинацией клавиш CTRL+. Или кнопкой Evaluate Symbolically (Вычислить аналитически) на панели инструментов Evaluation (Вычисление).
5. Щелкните за пределами данного блока, и программа MathCad произведет аналитическое решение системы уравнений.
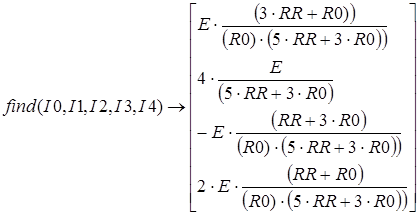
Полученный результат позволяет провести полный анализ схемы.
Задача 2. Найти все корни уравнения:

Анализ. Это уравнение четвертого порядка. Легко подобрать один корень (у = 1). Остающееся уравнение третьего порядка не имеет рациональных корней, так что поиск других корней этого уравнения — дело непростое. Неясно даже, сколько еще действительных корней имеет данное уравнение. Результаты численного решения зависят от подбора начального приближения и поэтому не гарантируют отыскания всех корней уравнения. Мы же решим это уравнение аналитически.
6. Введите заданное уравнение. Чтобы раскрыть скобки, дайте команду Symbolics > Simplify (Аналитические вычисления > Упростить).
7. Выделите в полученном уравнении независимую переменную (в данном случае у) и дайте команду Symbolics > Variable > Solve (Аналитические вычисления > Переменная > Решить).
Программа MathCad выдаст вектор, элементами которого являются корни данного уравнения.
8. Полученный результат содержит сложные комплексные радикалы, и его невозможно применить с пользой (нельзя даже точно сказать, являются ли корни действительными или комплексными). Чтобы разделить действительную и мнимую части, выделите результат вычисления целиком и дайте команду
Symbolics > Evaluate > Complex (Аналитические вычисления > Вычислить > В комплексном виде). В результате запись станет более простой, но результат все-таки останется трудным для восприятия.
9. Следующий шаг — раскрытие скобок, в данном случае упрощение аргументов тригонометрических функций. Для этого примените команду Symbolics > Expand (Аналитические вычисления >Раскрыть). Только теперь станет ясно, что все корни уравнения действительные (все мнимые компоненты сократятся). Это наилучшая точная запись решения, которую можно получить с помощью программы MathCad.
10.Чтобы получить результат в числовом виде, достаточно ввести в конце выражения (итогового или на любой из предыдущих стадий) команду вычисления (=).
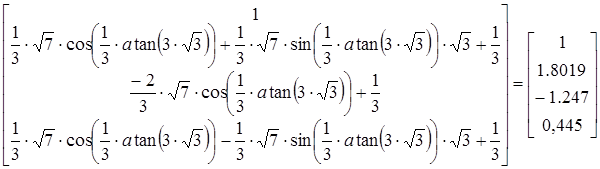
 Мы научились использовать программу MathCad для выполнения аналитических вычислений. Это позволяет получать точные решения задач, содержащих переменные параметры, анализировать полученные результаты, а также получать полный набор решений для некоторых типов уравнений.
Мы научились использовать программу MathCad для выполнения аналитических вычислений. Это позволяет получать точные решения задач, содержащих переменные параметры, анализировать полученные результаты, а также получать полный набор решений для некоторых типов уравнений.

Дата добавления: 2016-09-26; просмотров: 1788;











