Практическое занятие

Упражнение 18.1. Простые вычисления с использованием

Программы MathCad

Задача.Найти ребро куба, равновеликого шару, площадь поверхности которого равна площади боковой поверхности прямого кругового конуса, у которого высота вдвое меньше, чем длина образующей. Объем этого конуса равен 1.

Анализ.Основные геометрические формулы, используемые при расчете.

Объем конуса -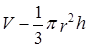

Площадь боковой поверхности конуса — S = prl.

Соотношение в конусе между радиусом основания, высотой и длиной образующей — r² + h² = l².

Площадь поверхности шара — V= 4pR².

Объем шара — V= 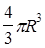. Объем куба — V= a³.

1.Запустите программу MathCad через Главное меню (Пуск > Программы > MathSoft Apps > MathCad).

2.Откройте панель инструментов Arithmetic (Счет) щелчком на кнопке Arithmetic Toolbar (Панель инструментов Счет) на панели инструментов Math (Математика) или с помощью команды View > Toolbars > Arithmetic (Вид > Панели инструментов > Счет).

3.Для удобства расчета будем обозначать каждую из вычисляемых величин отдельной переменной. Объем конуса обозначим как У и присвоим ему значение 1. Оператор присваивания вводится символом «:» или кнопкой Assign Value (Присвоить значение) на панели инструментов Arithmetic (Счет). Итак, надо ввести V: 1. В документе появится полноценный оператор присваивания:

V:= 1.

4. Путем несложных преобразований получим, что радиус основания конуса можно вычислить по формуле

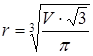
Вводить эту формулу следует слева направо. Порядок ввода этой формулы следующий: Сначала вводим знак корня произвольной степени: кнопка Nth Root (Корень данной степени) на панели инструментов Arithmetic (Счет) или комбинация клавиш CTRL+V Щелкните на черном квадратике, стоящем на месте показателя степени, и введите цифру 3. Щелкните на квадратике, замещающем подкоренное выражение, нажмите клавиши [V][*]. Введите знак квадратного корня: кнопка Square Root (Квадратный корень) на панели инструментов Arithmetic или клавиша [\] — и цифру 3. Прежде чем вводить знаменатель, дважды нажмите клавишу ПРОБЕЛ. Обратите внимание на синий уголок, который указывает на текущее выражение. Предполагается, что знак операции связывает выбранное выражение со следующим. В данном случае это безразлично, но в целом этот прием позволяет вводить сложные формулы, избегая ручного ввода дополнительных скобок. Нажмите клавишу [/]. Чтобы ввести число p, можно воспользоваться комбинацией клавиш CTRL+SHIFT+P или соответствующей кнопкой на панели инструментов Arithmetic (Счет).

На экране появится следующая надпись:

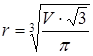
5. Введите формулы для вычисления длины образующей и площади боковой поверхности конуса:

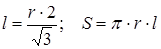
Указание знака умножения между переменными обязательно, так как иначе MathCad сочтет, что указана одна переменная с именем из нескольких букв.

6. Для вычисления радиуса шара R введите формулу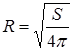

7. Для вычисления объема шара введите формулу .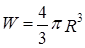

Использовать переменную V во второй раз не следует, так как теперь мы определяем совершенно другой объем.

8. Заключительная формула 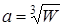позволит получить окончательный результат. После этого снова наберите имя переменной а и нажмите клавишу = или щелкните на кнопке Evaluate Expression (Вычислить выражение) на панели инструментов Arithmetic (Счет). После формулы появится знак равенства и вычисленный результат.

a = 0.7102

Вычислять можно как действительные, так и комплексные выражения. Обозначение мнимой единицы (i) следует вводить непосредственно после числового коэффициента, который нельзя опускать, даже если он равен единице.

9. Вернитесь к самому первому выражению и отредактируйте его. Вместо значения 1 присвойте переменной значение 8. Сразу же перейдите к последней введенной формуле и обратите внимание, что результат расчета сразу же стал отражать новые начальные данные.

Мы познакомились с методикой простейших вычислений в программе MathCad. Описанная техника позволяет использовать эту программу как «интеллектуальный калькулятор» для автоматического расчета по известным формулам. Особенностью программы MathCad является возможность практически мгновенного перерасчета с другими начальными данными.

Упражнение 18.2. Физические вычисления с использованием

Единиц измерения

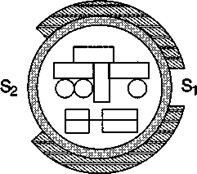
Постановка задачи. Теплоизолированный космический аппарат, находящийся на орбите Земли, имеет на борту приборы с электрической мощностью, которая может изменяться в ходе работы от N₁ = 75 Вт (дежурный режим) до N₂ = 200 Вт (сеанс связи). С целью обеспечения предсказуемого теплового режима в теплоизоляции сделано отверстие площадью S₁, на которое попадает поток солнечной энергии W = 1400 Вт/м². Полученная энергия излучается аппаратом через это и дополнительное отверстие в теплоизоляции с площадью S₂ в режиме «черного тела». Каковы должны быть площади отверстий, если допустимый диапазон температур для оборудования, расположенного в аппарате, составляет 20-30°С?

Анализ задачи.Минимальная температура аппаратуры соответствует режиму минимального тепловыделения. В этом случае поступающая мощность Q_l = WS₁ + N₁. Излучаемая мощность Q₂ = sT⁴₁ (S₁ + S₂), где Т₁ — минимальная допустимая температура в градусах Кельвина. В условиях теплового баланса эти мощности должны быть равны.

Режим максимального тепловыделения соответствует максимальной температуре аппаратуры. В этом случае WS₁ + N₂ = sT⁴₂ (S₁ + S₂),.

Используя два полученных уравнения, получаем:

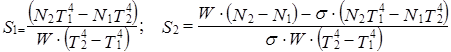
1. Запустите программу MathCad.

2. Введите значения известных величин, присвоив их переменным с соответствующими именами. Вместо нижних индексов используйте просто дополнительную цифру в названии переменной.

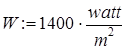
N1 := 75×watt N2 := 200×watt,

T1 := (20 + 273)×K T2 := (30 + 273)×K.

3. Обозначения физических единиц присоединяйте к соответствующим значениям через знак умножения. Если нужное обозначение неизвестно, используйте команду Insert > Unit (Вставка > Единица измерения). Измеряемая величина выбирается в списке Dimension (Размерность), а нужная единица измерения — в списке Unit (Единица измерения).

4. Присвойте переменной s значение постоянной Стефана-Больцмана

.

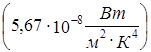Чтобы ввести греческую букву, используйте панель инструментов Greek (греческий алфавит) или введите соответствующую латинскую букву (в данном случае «s») и сразу же нажмите комбинацию клавиш CTRL+G. Так как специальной единицы для размерности этой константы не существует, ее следует составить из стандартных единиц методом умножения и деления.

5. Введите полученные в ходе анализа формулы для вычисления площадей отверстий, присвоив полученные значения переменным S₁и S₂.

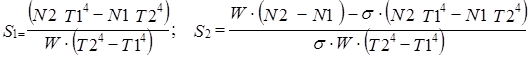
6. Чтобы увидеть результаты вычислений, введите имя первой из рассчитанных переменных и нажмите клавишу [=]. Затем проделайте то же самое со второй переменной.

S1 = 0.5679 m² S2 = 1.514 m²

7. Изменение значений параметров, заданных в условии задачи, приводит к автоматическому перерасчету формул. В частности, исследуйте, изменяя значение переменной W, как изменяются требования к такому методу терморегуляции при удалении аппарата от Солнца и приближении к нему (на орбите Венеры 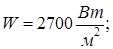на орбите Марса ).

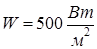8. Обратите внимание, что результат содержит единицы измерения в соответствии с системой единиц СИ. Используемая система единиц отображается в диалоговом окне Insert Unit (Вставка единиц измерения).

9. Чтобы изменить используемую систему единиц, дайте команду Math > Options (Математика > Параметры) и в открывшемся диалоговом окне Math Options (Параметры расчета) выберите вкладку Unit System (Система единиц). Выберите систему CGS и посмотрите, как изменились результаты (они теперь выражаются в квадратных сантиметрах). Если выбрать американскую систему единиц (U.S.), то результат будет выражен в квадратных футах.

Мы научились производить вычисления с использованием реальных размерных физических величин, а также производить преобразование данных из одной системы единиц в другую. Это позволяет немедленно получать результат в наиболее удобной форме.

Упражнение 18.3. Векторы и матрицы

Задача.Разложить вектор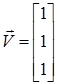

по нормированным собственным векторам матрицы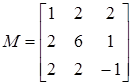

Анализ.Первый этап решения задачи состоит в нахождении собственных значений и собственных векторов данной матрицы. Затем необходимо найти вектор Т, такой что S×T = V, где S — матрица, столбцы которой представляют собой собственные вектора матрицы М.

1. Запустите программу MathCad.

2. Создайте матрицу М. Начните запись оператора присваивания, а для ввода правой части нажмите комбинацию клавиш CTRL+M, воспользуйтесь командой Insert >Matrix (Вставка > Матрица) или щелкните на кнопке Matrix or Vector (Матрица или вектор) на панели инструментов Matrix (Матрица).

3. В открывшемся диалоговом окне Insert Matrix (Вставка матрицы) укажите число строк и столбцов (по три) и щелкните на кнопке ОК.

4. Введите значения элементов матрицы в отведенные места.

5. Аналогичным образом сформируйте вектор V. Он будет представлять собой матрицу, имеющую только один столбец.

6. Собственные значения квадратной матрицы можно получить при помощи функции eigenvals. Результатом ее работы является вектор собственных значений, присвойте его переменной L.

7. Функция eigenvec позволяет получить собственный вектор, соответствующий данному собственному значению. Ей нужны два параметра: матрица, для которой ищется собственный вектор, и собственное значение, которому он соответствует. Чтобы записать собственные вектора в качестве столбцов матрицы S, надо при воить вычисленное значение столбцу матрицы. Столбцы матрицы в программе MathCad выбираются специальным верхним индексом, заключенным в угловые скобки. Чтобы ввести номер столбца, нажмите комбинацию клавиш CTRL+6 или щелкните на кнопке Matrix Column (Столбец) на панели инструментов Matrix (Матрица), после чего введите номер нужного столбца матрицы. Будьте внимательны — столбцы и строки матрицы нумеруются начиная с нуля.

S^<0>

8. В правой части оператора присваивания надо указать собственное значение матрицы. Собственные значения являются элементами вектора L. Номер элемента указывается как нижний индекс. Для ввода нижнего индекса нажмите клавишу [ или воспользуйтесь кнопкой Subscript (Индекс) на панели инструмен тов Matrix. Итоговый оператор для первого собственного вектора будет выглядеть следующим образом:

^S<0> := eigenvec(M,L₀).

Аналогично задайте операторы для второго и третьего собственных значений.

9. Для нахождения коэффициентов при собственных векторах в разложении необходимо решить систему линейных уравнений. Ее удобно записать в матричной форме. Создайте вектор Тс тремя элементами. Величины этих элементов значения не имеют.

10.Запишите ключевое слово given.

11.Ниже запишите матричное уравнение S- Т= V. Знак логического равенства введите с помощью комбинации клавиш CTRL+=.

12.Найдите коэффициенты в разложении при помощи функции find.

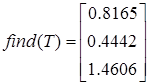
Мы научились производить операции с векторами и матрицами, использовать соответствующие функции, выделять столбцы матриц и отдельные элементы. Матричная запись часто позволяет представить задачу в более удобной форме.