Анализ эффекта Комптона

Известен факт увеличения длины волны отраженных фотонов. Наиболее надежно и точно он фиксируется в эффекте Комптона. При этом, в соответствии с законом локализации фотонов 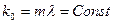, масса 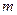отраженных фотонов уменьшается. Это однозначно свидетельствует о потере массы, а значит - и энергии фотоном. Если владелец потерянной массы остаётся неизвестным, то эффект Комптона становится ярким доказательством нарушения закона сохранения энергии и этот факт невозможно опровергнуть никакими косвенными экспериментами, доказывающими обратное.

Мы уже отметили, что дисбаланс масс ядер при их синтезе объясняется излучением гамма фотонов протонами. Что же касается причины дисбаланса масс фотонов в эффекте Комптона, то этот вопрос не ставился. Поэтому поставим его и попытаемся найти ответ или, в крайнем случае, сформулировать гипотезу о судьбе массы, теряемой отраженным фотоном.

На рис. 148 показана схема экспериментальной установки для изучения эффекта Комптона, а на рис. 149 – схема изменения длины волны отраженных фотонов при изменении угла 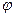. В эксперименте использовались рентгеновские фотоны с длиной волны .

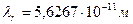Как видно (рис. 149), при увеличении угла рассеяния 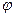интенсивность несмещенной линии 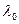падает, а интенсивность смещенной линии 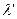возрастает.

Рис. 148. Схема для изучения эффекта Комптона:

1-рентгеновская трубка;

2-свинцовые экраны с прорезями; 3-фотопленка

Чтобы найти математическую модель, описывающую изменение длины волны отраженного фотона, надо знать, прежде всего, геометрические параметры взаимодействующих объектов – рентгеновских фотонов и электронов.

Известно, что длина волны рентгеновского фотона равна радиусу его вращения и изменяется в интервале 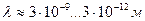. Длина волны, а значит и радиус свободного электрона равны 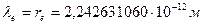. Конечно, при энергетических переходах электрона в атоме длина его волны изменяется. Однако эти изменения у поверхностных электронов настолько незначительны, что в данном случае ими можно пренебречь. Сравнивая длину волны рентгеновского фотона, использованного в эксперименте, 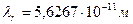и длину волны электрона 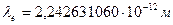, видим их близкие значения (табл. 4).

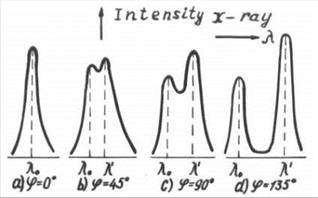
Рис. 149. Схема изменения длины волны отраженных фотонов от угла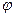

На рис. 150 приведены спектры ( 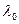и 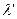), рассеянные под одним и тем же углом различными веществами. Главный вывод, который следует из этого рисунка, при возрастании атомного номера химического элемента вещества интенсивность несмещенной линии P возрастает, а интенсивность смещенной линии M падает. Так, у лития максимальная интенсивность излучения состоит из смещенной М составляющей, а у меди наоборот, интенсивность несмещенной линии P значительнее интенсивности смещенной линии M.

А теперь обратим внимание на рис. 150 и попытаемся найти ответ на вопрос: почему интенсивность смещённой линии падает с увеличением номера химического элемента?

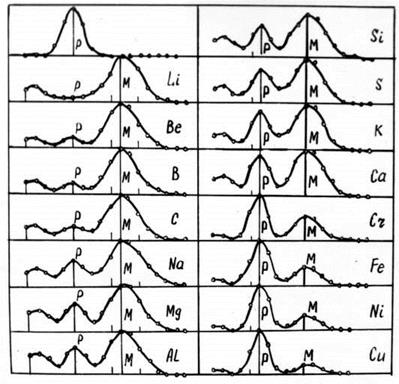
Рис. 150. Эффект Комптона на радиаторах различной природы

Ответ на этот вопрос следует из рис. 79, на котором показано ядро и атом лития. Нетрудно видеть, что поверхность такого атома почти пуста и у рентгеновских фотонов имеется возможность взаимодействовать с отдельными электронами.

При увеличении номера химического элемента увеличивается заполнение поверхностей атомов электронами, что затрудняет взаимодействие рентгеновских фотонов с отдельными электронами, в результате интенсивность смещенной линии (рис. 150) уменьшается.

Если представить атом меди, ядро которого показано на рис. 67, то его поверхность заполнена электронами полнее, что затрудняет взаимодействие рентгеновских фотонов с отдельными электронами и интенсивность смещенной линии уменьшается, что и наблюдается на рис. 150.

У нас есть основания представить поверхность многоэлектронного атома в виде одуванчика (рис. 151, b). Тогда поверхность такого атома, заполненная электронами, будет близка к сферической, когда он находится в невозбуждённом состоянии. Когда же один из его электронов поглощает фотон, то энергия связи такого электрона с ядром уменьшается, в результате он удаляется от ядра и от общей сферической поверхности атома. В таком состоянии он становится активным – готовым вступить в связь с аналогичным электроном другого атома. Так образуется молекула.

а)	b) Рис. 151. (a – модель ядра атома меди; (b) – возможная архитектоника поверхности многоэлектронного атома

Конечно, соединение произойдёт лишь с тем электроном соседнего атома, который будет удалён от его поверхности и у которого свободным будет противоположный магнитный полюс. Указанные два электрона и являются валентными электронами.

Таким образом, сравнивая поверхности атома лития (рис. 79) и атома меди (рис. 151, b), видим значительную возможность рентгеновских фотонов взаимодействовать индивидуально с электронами атома лития и меньшую - с электронами атома меди. Экспериментальные данные, представленные на рис. 151, убедительно подтверждают это.

А теперь проверим реализацию закона сохранения энергии в эффекте Комптона. Из формулы (88) следует, что изменение длины волны 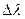отраженного фотона зависит от угла 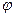(рис. 148, 149). В соответствии с константой локализации фотона 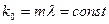при увеличении длины волны 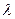фотона уменьшается его масса 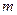, поэтому мы можем вычислить массу, потерянную рентгеновским фотоном при отражении.

Обозначая массу фотона до отражения через 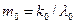, а после отражения – через 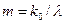и учитывая, что

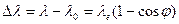, (271)

найдём

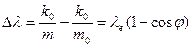, (272)

или

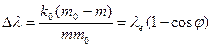. (273)

Если 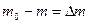, то

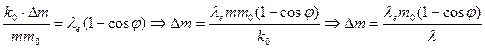. (274)

Длина волны рентгеновских фотонов, использованных в эксперименте, 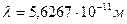. Константа локализации 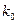(12) позволяет определить их массу

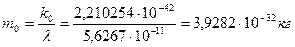. (275)

Поскольку угол 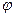может изменяться в интервале 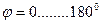, то для расчётов возьмём его среднее значение 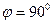. Тогда

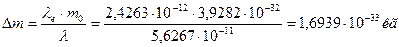. (276)

Таким образом, рентгеновский фотон, взаимодействуя с электроном под углом 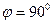, потерял

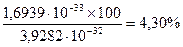(277)

своей массы. Тем не менее, если бы из потерянной массы сформировался фотон, то он имел бы радиус

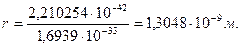(278)

Как видно, масса (276), потерянная отражённым рентгеновским фотоном, эквивалентна массе рентгеновского фотона (табл. 3).

Сразу возникает вопрос: куда девалась масса, потерянная отражённым рентгеновским фотоном, если она не сформировалась в соответствующий фотон? Конечно, если бы она сформировалась в соответствующий фотон, то приборы обязательно зарегистрировали бы его. Однако чёткой информации об этом нет, поэтому у нас появляются веские основания полагать, что масса, потерянная отражённым фотоном, не оформившись ни в какую частицу, растворилась в пространстве, приняв форму и свойства эфира.

Если это так, то сразу следует другой, не менее важный вопрос: выполняется ли закон сохранения энергии в эффекте Комптона?

Если при отражении фотонов с другими длинами волн закономерность изменения массы сохраняется, то при отражении реликтового фотона 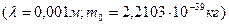, получим

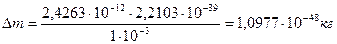. (279)

Так как реликтовый фотон с 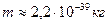является предельным (табл. 3), то фотоны с массой 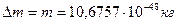не формируются. Электромагнитная субстанция, представляющая эту массу, не оформившись в фотон, растворяется в пространстве. В результате закон сохранения энергии не соблюдается. Эффект Комптона – убедительное доказательство нарушения закона сохранения энергии в его современной формулировке.

Таким образом, есть все основания поставить под сомнение результаты ряда косвенных экспериментов, доказывающих, что закон сохранения энергии при эффекте Комптона соблюдается.