Цилиндрические проекции.

При построении цилиндрических проекций представляют, что узловые точки, а значит, и линии сетки, проектируются с шаровой поверхности глобуса на боковую поверхность цилиндра. Цилиндрические проекции бывают нормальными (ось цилиндра совпадает с осью глобуса), косыми (ось цилиндра составляет с осью глобуса острый угол) и поперечными (ось цилиндра перпендикулярна оси глобуса). Диаметр цилиндра может быть равен диаметру глобуса (касательный цилиндр) или может быть меньше него (секущий цилиндр).

Виды цилиндрических проекций:

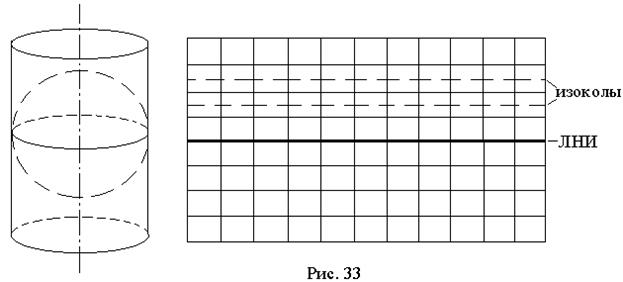
1. Нормальная цилиндрическая картографическая сетка на касательном цилиндре.

Все линии сетки прямые, меридианы перпендикулярны параллелям и отстоят друг от друга на равных расстояниях. Линией нулевых искажений (ЛНИ) служит экватор, а изоколы (линии равных искажений) имеют форму прямых, параллельных экватору; с удалением от экватора искажения возрастают (рис. 33).

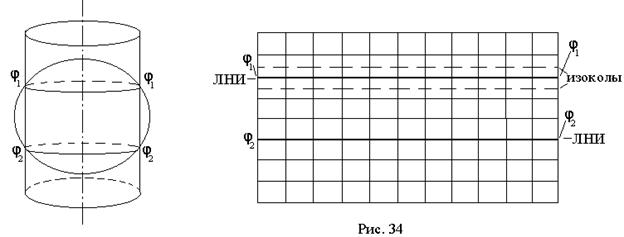
2. Нормальная сетка на секущем цилиндре имеет две линии нулевых искажений, расположенных вдоль параллелей сечения цилиндра с глобусом (рис. 34).

3. Косая цилиндрическая сетка на секущем цилиндре имеет в северной части линию нулевых искажений в форме прямой, перпендикулярной к среднему меридиану карты. Внешний вид сетки представлен кривыми линиями меридианов и параллелей.

4. Примером поперечной цилиндрической проекции может служить проекция Гаусса-Крюгера, в которой каждый поперечно расположенный цилиндр используется для проектирования поверхности одной зоны Гаусса.

Примеры цилиндрических проекций:

а) Цилиндрическая прямоугольная проекция на секущем цилиндре. Линии нулевых искажений – параллели с широтами j₁ и j₂. Между ними происходит «сжатие» поверхности глобуса и показатели искажений меньше 1. На внешних участках сетки они больше 1.

б) Цилиндрическая нормальная равноугольная проекция Меркатора на касательном цилиндре. В ее основе лежит свойство равноугольности – нет искажения углов и форм малых фигур. Линия нулевых искажений – экватор. С удалением от него увеличиваются искажения длин и площадей.

в) Цилиндрическая нормальная произвольная проекция Урмаева. В ней промежутки по меридианам между параллелями растягиваются не так сильно, как в проекции Меркатора. Этим достигается уменьшение искажений площадей, но теряется свойство равновеликости.