Устойчивость подкрепленных пластин

Исследование устойчивости пластин, подкрепленных однонаправленным или перекрестным набором стрингеров, можно осуществлять на основе различных расчетных моделей.

Наиболее простая и распространенная - конструктивно-ортотропная модель, в которой жесткость стрингеров как бы “размазывают” по пластине, присоединяя ее к жесткости самой пластины. В результате пластина приобретает в разных направлениях разные свойства и становится “ортотропной”. Исследование устойчивости таких пластин ведут на основе уравнений и соотношений теории ортотропных пластин.

Проблема здесь состоит только в том, чтобы грамотно свести дискретно-подкрепленную пластину к гладкой ортотропной. Очевидно, что приемлемую точность результатов здесь можно ожидать только при достаточно часто расположенных одинаковых стрингерах (регулярный набор). Явление местной потери устойчивости подкрепленной панели, выражающееся в выпучивании “обшивки” между прямолинейными стрингерами в такой модели получить невозможно.

Пример с регулярно подкрепленной пластиной.

- Одинаковые, регулярно закрепленные слои заменяем сплошным слоем с некими приведенными свойствами.

- Для этого слоя справедлива гипотеза Кирхгоффа о жесткой нормали.

- Ребра и их слой воспринимают только продольные напряжения, на сдвиг работает только обшивка.

Примем для такой панели (Рис.18.3) внутреннюю поверхность за начальную.

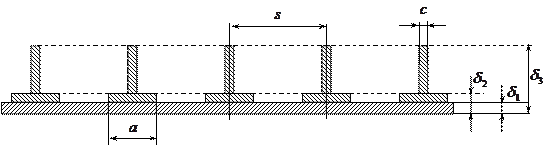Получим три слоя: реальный, с толщиной обшивки 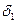, и два условных (показаны пунктиром)

(Рис.18.3)

Тогда в стандартных формулах для коэффициентов жесткости ортотропного материала

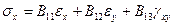
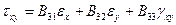
следует принять:

1) в слое (1) 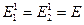, , 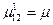, 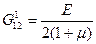где E, 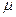- параметры обшивки,

то есть , , ,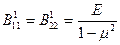

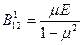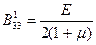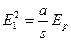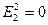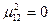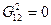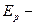2) в слое (2) , , , , где модуль ребер,

то есть , ,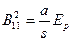

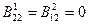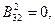
3) в слое (3) , ,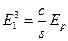

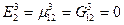то есть , .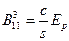

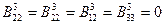При этих коэффициентах жесткости для усилий в панели, интегрируя напряжения по поперечному сечению, получаем

,

,

,

,

,

.

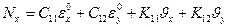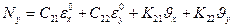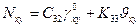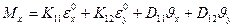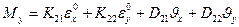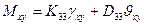Жесткости принимают теперь вид:

,

, , ,

, , ,

, ,

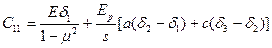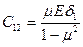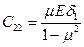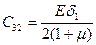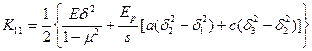
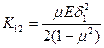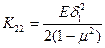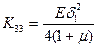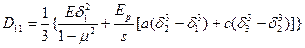
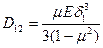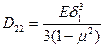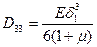
Параметры 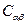называются мембранными, 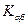- смешанными, а 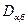- изгибными.

Отметим еще одно важное обстоятельство. Если для поверочных расчетов конструктивно-ортотропная модель может иногда давать удовлетворительные результаты, то для рационального проектирования панелей (с целью найти наиболее выигрышный в весовом отношении и, естественно, нерегулярный набор стрингеров) такая модель вовсе непригодна. Учет же дискретности расположения подкрепляющего набора выливается в очень сложную задачу.

Рассмотрим использующиеся здесь модели и подходы.

Почти все они предполагают, что взаимодействие стрингеров с пластиной происходит по некоторым линиям контакта 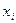(рис.18.4) даже, если стрингер изготовлен “зацело” с пластиной или наоборот - скреплен с ней точечно - заклепками.

Самый наглядный подход - с позиции контактных задач - стрингеры отделяются от пластины, по линиям взаимодействия прикладываются неизвестные контактные усилия. Решения для пластины и стрингеров от этих усилий “склеиваются” по перемещениям. При этом могут приниматься самые разнообразные допущения о работе стрингеров и характере их взаимодействия с пластиной.

Рассмотрим наипростейший пример. Пусть пластина подкреплена одним стрингером. Воспользуемся решением в одинарных рядах

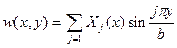. (18.13)

Из общей симметрии задачи очевидно, что решение может быть только симметричным, либо кососимметричным относительно оси 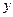. При косой симметрии изогнутой поверхности линия 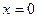не изгибается и фактически оказывается как бы шарнирно опертым ребром. Критическое напряжение такой формы потери устойчивости

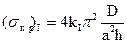, (18.14)

где 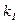представлены на рис.14.2.

Осталось рассмотреть симметричную форму. Для этого случая общее решение вида (14.12)

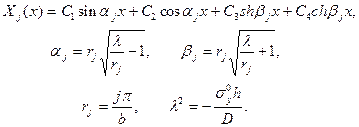(18.15)

следует подчинить условиям опирания края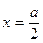

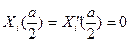(18.16)

и условиям на линии .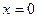

Первое условие - условие симметрии, которое дает

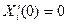. (18.17)

Второе - условие контакта со стрингером. Его смысл: обобщенная перерезывающая сила в пластине

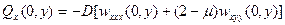(18.18)

удваивается и прикладывается к стрингеру, для которого пишем уравнение изогнутой оси с учетом сжимающей силы

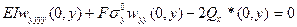
или с учетом (18.15),(18.6)

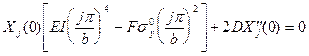. (18.19)

Подчинив (18.15) условиям (18.16), (18.17), получим однородную систему относительно констант 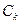. Равенство нулю определителя этой системы дает характеристическое уравнение для определения собственных значений

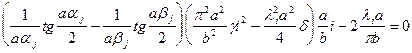, (18.20)

где введены безразмерные параметры .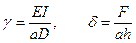

Наименьший из корней трансцендентных уравнений дает

.

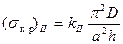Значения 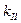, которые можно назвать коэффициентами общей потери устойчивости (рис.18.6 правый), а также 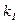, которые определяют как бы местную потерю устойчивости (рис.18.3 левый), представлены ниже.

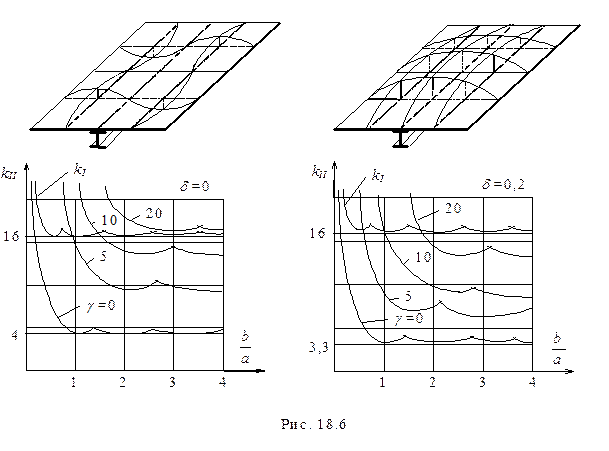
Из графиков ясно, что в зависимости от сочетания жесткостей стержня и пластины потеря устойчивости может произойти как по форме I, так и по форме II. Рационально спроектированная пластина не должна иметь “запаса устойчивости” одной формы по отношению к другой, поэтому стержня, т.е. следует выбирать и условие равенства при заданном удлинении 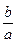пластины.

Отметим один любопытный факт. Если стержень обладает очень малой изгибной жесткостью 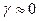, то его наличие, сказывающееся в 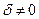, опускает 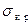подкрепленной пластины ниже 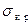гладкой, что выглядит парадоксально. Объяснение простое - снижается 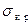, а не

.

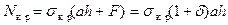Подход с позиций контактных задач, приемлемый для одного - двух стрингеров, в крайнем случае - для регулярного набора, делает расчет для нерегулярного набора весьма сложным.

В этих случаях, как правило, строят приближенные решения на основе вариационных методов, перебирая всевозможные формы потери устойчивости и вычисляя 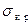из условия минимума полной суммарной энергии пластины и ребер на этих перемещениях.